复习六——解斜三角形

第二十七教时

教材：复习六——解斜三角形

目的：巩固对正弦、余弦的掌握，并能较熟练地应用解决具体问题。

过程：

一、复习：1°两个定理　 2°两个定理能解决的问题

二、  例题：

1．证明射影定理：a = bcosC + ccosB；b = acosC + ccosA；c = acosB + bcosA

证一：右边 == 左边

证二：右边 = 2RsinBcosC + 2RsinCcosB=2Rsin(B+C)=2RsinA= a = 左边

其余两式同

2．已知：在△ABC中，ÐA=45°，AB=，BC=2，解此三角形。

解一：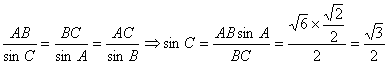

　　　∴当ÐC = 60°时,　ÐB = 75°　 ∴

∴当ÐC = 120°时,　ÐB = 15°　 ∴

　　　　 解二：设AC = b，由余弦定理：

即：　　解得：

再由余弦定理：　∴ÐC = 60°或120°, ÐB = 75°或15°

3．在△ABC中，若，判断△ABC的形状。

解一：由正弦定理：

∴2A = 2B 或 2A = 180° - 2B　即：A= B 或 A + B = 90°

∴△ABC为等腰或直角三角形

解二： 由题设：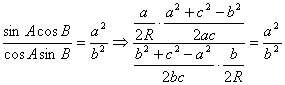

化简：b²(a² + c² - b²) = a²(b² + c² - a²)　∴(a² -b²)(a² + b² - c²)=0

∴a = b或 a² + b² = c²　 ∴△ABC为等腰或直角三角形

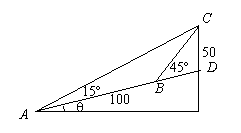
4．如图：在斜度一定的山坡上的一点A测得

山顶上一建筑物顶端C对于山坡的斜度为

15°，向山顶前进100m后，又从点B测得

斜度为45°，假设建筑物高50m，

求此山对于地平面的斜度q。

解：在△ABC中，AB = 100m ,  ÐCAB = 15°,　ÐACB = 45°-15° = 30°

由正弦定理：　 ∴BC = 200sin15°

在△DBC中，CD = 50m ,  ÐCBD = 45°,　ÐCDB = 90° + q

由正弦定理：Þcosq =　∴q = 42.94°

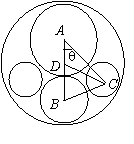
5．一块直径为30cm的圆形铁板，已经截去直径分

别为20cm，10cm的圆形铁板各一块，现要求

在所剩余的铁板中，再截出同样大小的铁板两块，

问：这两块铁板的半径最大有多少cm？

解：设所求最大圆的半径为x，

则在△ABC中：

又在△ACD中：

∴

6．某船在海上航行中不幸遇险，并发出呼救信号，我海上救生艇在A处获悉后，立即测出该船的方位角为45°，与之相距10 nmail的C处，还测得该船正沿方位角105°的方向以每小时9 nmail的速度向一小岛靠近，我海上救生艇立即以每小时21 nmail的速度前往营救，试求出该海上救生艇的航向及与呼救船相遇所需时间。

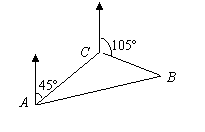解：设所需时间为t小时，

在点B处相遇（如图）

在△ABC中，ÐACB = 120°,　

AC = 100,　AB = 21t,　BC = 9t

由余弦定理：(21t)² = 10² + (9t)² - 2×10×9t×cos120°

整理得：36t² -9t - 10 = 0 　 解得：（舍去）

由正弦定理：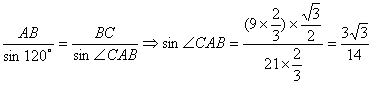

∴ÐCAB = 21°47’

7．在湖面上高h处，测得云彩仰角为a，而湖中云彩影的俯角为b，

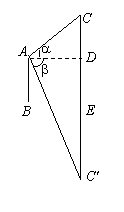求云彩高。

解：C、C’关于点B对称，设云高CE = x，

则CD = x - h，C’D = x + h，

在Rt△ACD中，

在Rt△AC’D中，

∴　　解得：

三、  作业： 《导学•创新》　§5.9　 §5.10