第二十五教时
教材：复习四——平面向量的数量积及运算律
目的：要求学生对平面向量的数量积的概念理解更清晰，并能教熟练地应用于平行、垂直等问题。
过程：
一、复习：
1．定义、其结果是一个数量。
2．a•b>0Û0≤q<90°；a•b=0Û=q=90° 即a^b；a•b<0Û90°<q≤180°
3．性质1° —5°
4．运算律
二、 例题：
1．已知a = 5，b = 8，a 与b的夹角为60°，求 a + b
解：a•b = abcos60° = 5×8×
= 20
∴a + b 2 = (a + b)2 = a2 + b2 + 2a•b = 129
∴a
+ b =
2．求证：a + b ≤a + b
证：a + b 2 = (a + b)2 = a2 + b2 + 2a•b = a2 + b2 + 2abcosq
≤ a2 + b2 + 2ab = ( a + b )2
即：a + b ≤a + b
3．设非零向量a、b、c、d，满足d = (a•c) b - (a•b)c，求证：a^d
证：内积a•c与a•b均为实数，
∴a•d = a•[(a•c) b - (a•b)c] = a•[(a•c) b] - a•[(a•b)c]
= (a•b)(a•c) - (a•c)(a•b) = 0
∴a^d
4．已知非零向量a、b，满足a ¹±b，
求证：b-a垂直于a+b的充要条件是a = b
证：由题设：b-a与a+b均为非零向量
必要性：设b-a垂直于a+b，则(b-a)(a+b) = 0
又：(b-a)(a+b) = b2 - a2 = b2 - a2
∴b2 - a2 = 0 即：a = b
充分性：设a = b，则(b-a)(a+b) = b2 - a2 = b2 - a2 = 0
即：(b-a)(a+b) = 0 ∴(b-a) ^ (a+b)
5．已知a、b都是非零向量，且a + 3b与7a - 5b垂直，
a - 4b与7a - 2b垂直，求a与b的夹角。
解：由(a + 3b)(7a - 5b) = 0 Þ 7a2 + 16a×b -15b2 = 0 ①
(a - 4b)(7a - 2b) = 0 Þ 7a2 - 30a×b + 8b2 = 0 ②
两式相减：2a×b = b2
代入①或②得：a2 = b2
设a、b的夹角为q，则cosq =
∴q = 60°
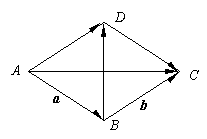
6．用向量方法证明：菱形对角线互相垂直。
证：设
=
= a , 
=
= b
∵ABCD为菱形 ∴a = b
∴
×
= (b + a)(b - a) = b2 - a2 = b2
- a2
= 0
∴^
7．如图，AD、BE、CF是△ABC的三条高，
求证：AD、BE、CF相交于一点。
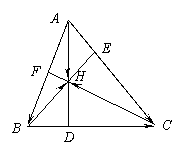证：设BE、CF交于一点H，
= a, = b, 
= h,
则
= h - a
, 
= h - b
, = b - a
∵^, ^
∴
∴^
又∵点D在AH的延长线上，∴AD、BE、CF相交于一点
三、 作业：《导学•创新》 §5.6