第二十二教时
教材：复习一——向量、向量的加法与减法、实数与向量的积
目的：通过复习对上述内容作一次梳理，使学生对知识的理解与应用提高到一个新的水平。
过程：
一、知识（概念）的梳理：
1．向量：定义、表示法、模、几种特殊向量
2．向量的加法与减法：法则（作图）、运算律
3．实数与向量的积：定义、运算律、向量共线的充要条件、
平面向量的基本定义
二、 例题：
1．若命题M：
=
；命题N：四边形ABB’A’是平行四边形。
则M是N的 （ C ）
(A)充分不必要条件 (B) 必要不充分条件
(C)充要条件 (D) 既不充分也不必要条件
解：若=，则 =，且, 方向相同
∴AA’∥BB’ 从而ABB’A’是平行四边形，即：MÞN
若ABB’A’是平行四边形，则AA’=BB’，且AA’∥BB’
∴=
从而=，即：NÞM
2．设A、B、C、D、O是平面上的任意五点，试化简：
1°
2°
3°
解：1° 原式= 
2° 原式= 
3° 原式= 
3．a =“向东走5km”，b =“向西走12km”，试求a+b的长度与方向。
解：如图：
(km)
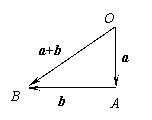tanÐAOB =
, ∴ÐAOB = arctan
∴a + b的长为13km，方向与
成arctan的角。
4．如图：1°已知a、b、c、d，求作向量a-b、c-d。
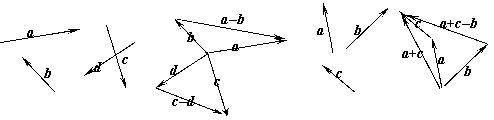2°已知a、b、c，求作a + c - b
5．设x为未知向量，a、b为已知向量，解方程2x-(5a+3x-4b)+
a-3b=0
解：原方程可化为：(2x - 3x)
+ (-5a +a) + (4b-3b)
= 0 ∴x =
a + b
6．设非零向量a、b不共线，c=ka+b，d=a+kb (kÎR)，若c∥d，试求k。
解：∵c∥d ∴由向量共线的充要条件得：c =λd (λÎR)
即：ka+b=λ(a+kb) ∴(k-λ)a + (1-λk)b = 0
又∵a、b不共线 ∴由平面向量的基本定理：
7．
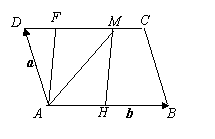
如图：已知在 ABCD中，AH=HD，BF=MC=
BC，设
=a，
=b，试用a、b分别表示
、
、
。
解：∵ ABCD中，BF=MC=BC,
∴FM=BC=AD=AH ∴FM AH
∴四边形AHMF也是平行四边形，∴AF=HM
又：
a ,
而
b
∴
= a +
b ,
= -b - a
-(-b - a) = b + a
三、 作业： 《导学•创新》§5.1 §5.2