高 一 数 学第二学期期末练习
一. 选择题：本大题共10个小题，每小题4分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。
1. 若
，则角x的终边位于（ ）
A. 第二、四象限 B. 第二、三象限
C. 第一、二象限 D. 第三、四象限
2. 求值：
等于（ ）
A. 
B.
C.
D.
3. 对于下列四个命题：①
；②
；③
；④
。其中正确命题的序号是（ ）
A. ①③ B. ①④ C. ②③ D. ②④
4. 已知
，则
等于（ ）
A. 
B.
C.
1 D.
2
5. 如图，在四边形ABCD中，下列各式成立的是（ ）
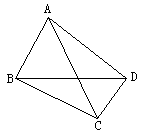
A. 
B. 
C. 
D. 
6. 已知
，则
与
的夹角为（ ）
A. 30° B. 45° C. 60° D. 90°
7. 已知
是任意两个向量，下列条件：①
；②
；③与的方向相反；④
或
；⑤与都是单位向量，其中为向量与共线的充分不必要条件的个数是（ ）
A. 1 B. 2 C. 3 D. 4
8. 在下列四个函数中，以
为最小正周期，且在区间
上为增函数的是（ ）
A. 
B.
C. 
D.
9. 下列命题中正确的命题是（ ）
A. 函数
的定义域是
B. 当
时，函数
的最小值是
C. 不存在实数
，使得函数
为偶函数
D. 为了得到函数
，
的图像，只需把函数
图象上所有的点向左平行移动
个长度单位
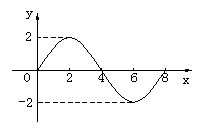
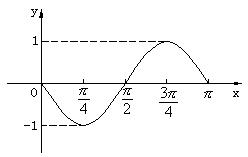
10. 下图是函数
一个周期的图像，则
的值等于（ ）
A. 
B.
C.
D.
二. 填空题：本大题共5个小题，每小题4分，共20分。把答案填在题中横线上。
11. 已知α，β为锐角，
，则
__________。
12. 已知
三点共线，则
__________。
13. 求值：
__________。
14. 已知点
，若
，则
______，______。
15. 函数
的定义域是______________________________，值域是______________________________。
三. 解答题：本大题共5个小题，共40分。解答应写出文字说明、证明过程或演算步骤。
16. （本小题满分8分）
在△ABC中，角A，B，C所对的边分别为a，b，c。若
，△ABC的面积
，求△ABC的外接圆的直径。
17. （本小题满分8分）
已知
。当k为何值时，
（I）
与
垂直；
（II）与平行，平行时它们是同向还是反向。
18. （本小题满分8分）
已知函数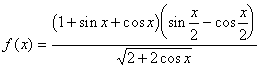
。
（I）当180°＜x＜360°时，化简函数
的表达式；
（II）写出函数的一条对称轴。
19. （本小题满分8分）
把函数的图像按
平移后得到函数
的图像。
（I）求函数的解析式；
（II）作函数
的图像（一个周期）。
20. （本小题满分8分）
是否存在锐角α，β，使得下列两式：①
；②
同时成立？若存在，求出α和β；若不存在，说明理由？
【试题答案】
一. 选择题：本大题共10个小题，每小题4分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。
1. A 2.A 3. B 4. D 5. C
6. C 7. C 8. D 9. B 10. A
二. 填空题：本大题共5个小题，每小题4分，共20分。把答案填在题中横线上。
11. 
12.
13. 
14. 
15. 
三. 解答题：本大题共5个小题，共40分。解答应写出文字说明、证明过程或演算步骤。
16. （本小题满分8分）
解：依题意
，得：
…………2分
由余弦定理得：
………………5分
又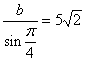
，△ABC的外接圆的直径为
………………8分
17. （本小题满分8分）
解：由已知
…………2分
因为与垂直，所以
得
解得：
即当时，两向量垂直………………5分
当与平行时，存在惟一的实数
，使得
则有
当
时，向量与平行
因为
，此时它们是反向………………8分
18.（本小题满分8分）
解：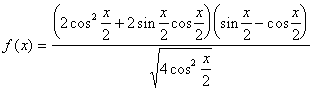
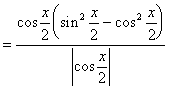…………………4分
因为
，
………………5分
………………6分
函数
的一条对称轴是
（答案不唯一，满足
）
………………8分
19. （本小题满分8分）
解：由平移公式得：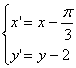
代入
得：
即函数
………………3分
………………5分
| x | 0 |
|
|
|
|
|
| 0 |
| 0 | 1 | 0 |
20. （本小题满分8分）
解：由得：
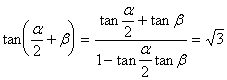………………3分
将②式代入得：
与②式联立，解得：
或
………………5分
当
时，因为
，这样的角
不存在，只能是
，
………………6分
因为
均为锐角，所以
………………8分
故存在锐角，使得①，②同时成立。