高一（上）数学期末试卷
一、选择题（每题3分，共36分）
1、如果A = 
，那么错误的结论是
（ ）
A 0
B {0}
A C 
D 
2、对于命题“3≥2”，规定p：“3>2”，q：“3=2”，那么下列四种认识正确的是 （ ）
A 命题是“p或q”的形式，并且是真命题
B 命题是“p或q”的形式，并且是假命题
C 命题是“p且q”的形式，并且是真命题
D 命题是一个简单命题，并且是假命题
3、下列四组中的函数f (x)与g ( x ),表示相同函数的一组是 （ ）
A
f ( x ) = 
, g ( x ) =(
)
B f( x )= 
, g(x) =
C f ( x ) = x
,
g ( x ) =
D f ( x ) = x, g ( x ) =
4、等差数列{a
}中，若a
=1,a
=5,则a
=
( )
A
7
B 9
C 
D 25
5、不等式
<0的解集是
（ ）
A {xx<-
, 或x>1}
B {xx<-1,或x>}
C
{x-<x<1}
D {x-1<x<}
6、函数y = -x(x≤0 )的反函数是
（ ）
A y = - 
( x≥0 ) B y = 
( x≤0)
C y = - ( x≤0) D y = -
( x≤0)
7、0．3，log
0.3,2
这三个数之间的大小顺序是
（ ）
A 0．3<2 < log0.3 , B 0．3 < log0.3 < 2
C log0.3 < 0．3 < 2 ,
D log0.3 <2 < 0．3
8、若集合S = 
，T = 
，则S∩T是
（ ）
A、S B、T C、 
D、 有限集
9、等比数列{a}中已知a+a
=2a，则公比q=
（ ）
A 1或
B 1或-
C 1或-2 D -
10、函数f(x) = logx- 2 (x≥1),则f
(x)的定义域是
（ ）
A、 R B、 
C、 
D、（0，1）
11、已知数列1，0，1，0，…，则不是它的通项公式的
是 （
）
A、 
B、
C、 +(n-1)(n-2) D、 
12、数列
是等差数列的充要条件是
（
）
A、 S
B、
C、
（a
D、
（a
二、填空题（每题4分，共24分）
13、若集合A={xx是菱形}，B={xx是矩形}，则A
B=
。
14、设函数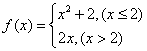
，则f(-4)= 。
15、函数y=
的单调递增区间是
。
16、方程㏒
(3x-1)=㏒(3-x)的解是
。
17、7+3与7-3的等比中项是
。
18、数列
的前n项和S=2n+1，则aa的值是
。
三、解答题 （19题 8分，20、21题各10分，22题12分，共40分）
19、解不等式׀2x-a׀≤1
20、已知满足a
=a+1
且
=1；
（1）
证明：数列{ a}是等差数列，并求a的表达式;
（2）
求数列{}的前n项和s.
21、某地方政府为保护国内电子工业发展，决定对某一进口电子产品征附加税，已知这种电子产品在国内市场零售价为每件250元，每年可销售40万件，若附加税率为每百元征x元时，则每年销售减少
x万件。
（1） 试将该产品一年的附加税额y 万元表示成 x 的函数；
（2） 若该项经营中政府在一年所得的税额不少于600万元，那么x应控制在什么范围内？
22、已知函数f(x)=㏒(2
-1),
（1） 求函数f(x)的定义域；
（2） 判断并证明函数f(x)的单调性；
（3）
解方程
；
高一（上）数学期末试卷
一、选择题
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| C | A | C | B | C | C | C | A | B | B | C | B |
二、填空题 ：
13、{x∣x是正方形} 。 14、 18 。 15、[1，+∞）。
16、1 。 17、 ±2。 18、18。
三、解答题：
19、解：原不等式可化为：-1≤2x-a≤1即a-1≤2x≤a+1∴
≤x≤
∴原不等式的解集为{x∣≤x≤}
20、解：（1）∵a=a+1∴a- a=1(常数) ∴数列{ a}是等差数列
∵=1，d=1∴a=1+(n-1)×1=n.
(2)
s=
=
=n
+n
21、解：（1）y=(40-x)×250x%=-4x+100x
(2) ∵ -4x+100x≥600∴x-25x+150≤0
∴10≤x≤15
∴附加税率x应控制在10≤x≤15。
22、解：（1）要使f(x) =㏒(2-1)有意义，则2-1>0
2>1x>0，
∴定义域为
(2 ) 设任意
，且
，则
f(x)-f(x)=㏒(2
-1)- ㏒(2
-1)= ㏒
，
0<∴1<2<2∴0<<1,
∴ ㏒<0即f(x) <f(x)
∴f(x)在上是增函数。
（3）由得：㏒（2
-1）=㏒（2+1）∴2=2
或2=-1（舍去）∴x = 1。