用二次函数的图象讨论二次方程根的分布
保定三中 尚玉伟
对一元二次方程![]() ,除了讨论其根的性质和符号外往往还要求我们讨论其根落在某个区间内或外的充要条件,这类问题,一般大都以二次函数的图象作为辅助工具。下面介绍借助二次函数图象讨论二次方程根的范围问题的一般方法。
,除了讨论其根的性质和符号外往往还要求我们讨论其根落在某个区间内或外的充要条件,这类问题,一般大都以二次函数的图象作为辅助工具。下面介绍借助二次函数图象讨论二次方程根的范围问题的一般方法。
对于方程![]() ,总可以化为与其同解的方程
,总可以化为与其同解的方程![]() 的形式。
的形式。
1.
程![]() 的根与常数
的根与常数![]() 的关系
的关系
设![]() 的二根为
的二根为![]() 、
、![]() ,且
,且![]() ,那么它们与常数
,那么它们与常数![]() ,在
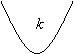
,在![]() 轴上的位置关系分别如下图:
轴上的位置关系分别如下图:
 | |||||
 | |||||
 | |||||
|
|
(1)两根均小于![]() ,即
,即![]() 的充要条件是
的充要条件是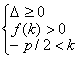
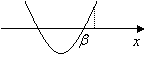
(2)一根小于![]() 而另一根大于
而另一根大于![]() ,即
,即![]() 的充要条件是
的充要条件是![]()
(3)二根均大于![]() ,即
,即![]() 的充要条件是
的充要条件是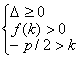
例1 设二次方程![]() 的解满足下列条件:(1)两根都大于1;(2)一根大于1,而另一根小于1,分别求实数
的解满足下列条件:(1)两根都大于1;(2)一根大于1,而另一根小于1,分别求实数![]() 的范围。
的范围。
2.方程![]() 的根与常数
的根与常数![]() 的关系
的关系
如果方程![]()
![]() 二根为
二根为![]() 、
、![]() ,且
,且![]() ,那么它们与常数
,那么它们与常数![]() ,在
,在![]() 轴上的位置关系分别如下图:
轴上的位置关系分别如下图:
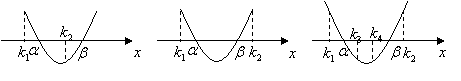 | |||
 | |||
(1)
方程![]() ,两根
,两根![]() 分别在
分别在![]() 两侧的充要条件是
两侧的充要条件是![]()
(2)方程![]() 在
在![]() 只有一根,即
只有一根,即![]() 或
或![]() 的充要条件是
的充要条件是![]() 或
或![]()
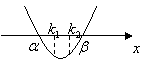
(3)方程![]() 二根都在
二根都在![]() 内,即
内,即![]() 的充要条件是
的充要条件是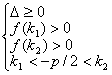
(4)方程![]() 二根
二根![]() 、
、![]() 满足条件
满足条件![]() 且
且![]() 的充要条件是
的充要条件是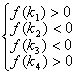
例2.若方程![]() 的二根满足条件,小根小于1,大根在(1, 3)内,求
的二根满足条件,小根小于1,大根在(1, 3)内,求![]() 的范围。
的范围。
一般说来,利用二次函数图象来研究与其相应的一元二次方程实根的分布问题,关键是根据题设条件作出抛物线的确切位置的草图,根据图列出满足条件的不等式。这要比直接利用判别式和根与系数的关系来解方便些。其优点是直观明显,公式与图形结合,有利于提高我们分析问题和解决问题的能力。
若二次方程的根分布在某闭区间上,这时区间端点的值要通过检验看是否满足题意。
作业:
1.方程![]() 的两根均大于2,求实数
的两根均大于2,求实数![]() 的范围。
的范围。
2.方程![]() 的两实数一根小于1,另一根大于1,求实数
的两实数一根小于1,另一根大于1,求实数![]() 的范围。
的范围。
3.方程![]() 的两实根都在(0, 1)内,求实数
的两实根都在(0, 1)内,求实数![]() 的范围。
的范围。
4.![]() 为什么数时,关于
为什么数时,关于![]() 的方程
的方程![]() 的两根
的两根![]() 、
、![]() 分别满足
分别满足![]() ,
,![]() 。
。