高一数学节节练
正余弦函数的图象和性质
第一课时:正余弦函数图象画法
1.画出下列函数的图象
①![]() ②
②![]()
2.![]() 和直线
和直线![]() 围成一个封闭的平面图形,则这个封闭的图形的面积为
围成一个封闭的平面图形,则这个封闭的图形的面积为
A、4
B、8
C、2![]() D、
D、![]()
3.求使![]() 的
的![]() 的取值范围
。
的取值范围
。
4.方程![]() 的实根个数为
。
的实根个数为
。
5.作出函数![]() 的简图。
的简图。
第二课时:主要性质:定义域与值域
1.求下列函数的定义域与值域:
![]() ;
;
2.求函数![]() 的值域;
的值域;
3.求函数![]() 的值域。
的值域。
4.函数![]() 的值域是( )
的值域是( )
A、![]() B、
B、![]() C、[0,2] D、[0,1]
C、[0,2] D、[0,1]
5.若函数![]() 的最大值为
的最大值为![]() 最小值为
最小值为![]() 求函数
求函数![]() 的最值。
的最值。
6.[思考题]:已知函数![]() 在
在![]() 上的最大值为1,求实数a的值。
上的最大值为1,求实数a的值。
7.求![]() 的最大值和最小值。
的最大值和最小值。
第三课时:主要性质:周期性
1.函数![]() 的最小正周期为
。
的最小正周期为
。
2.如下函数中,存在最小正周期的是( )
A、![]() B、
B、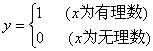
C、![]() D、
D、![]()
3.已知函数![]() 的定义域为R,且对于任意的
的定义域为R,且对于任意的![]() 有
有![]()
求证:函数![]() 为周期函数。
为周期函数。
4.已知函数![]()
(1)求函数![]() 的最小正周期;
的最小正周期;
(2)若![]() 时,
时,![]() 的最大值为1,求a的值。
的最大值为1,求a的值。
5.函数![]() 分别满足下列条件,能确定其为周期函数的是
。(所有正确的结论)
分别满足下列条件,能确定其为周期函数的是
。(所有正确的结论)
①![]() ;
②
;
②![]() ;
;
③![]() ; ④
; ④![]()
第四课时:主要性质:奇偶性与单调性
1.求下列函数的单调区间:
①![]() ②
②![]()
③![]() ④
④![]()
2.函数![]() 的部分图象是图中的
的部分图象是图中的
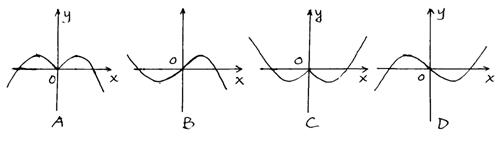
3.![]() ,若该函数是单调函数,求实数
,若该函数是单调函数,求实数![]() 的最大值。
的最大值。
4.如果函数![]() 的图象关于直线
的图象关于直线![]() 对称,那么
对称,那么![]() =( )
=( )
A、![]() B、
B、![]() C、1
D、
C、1
D、![]()
5.当![]() = 时,函数
= 时,函数![]() 为奇函数。
为奇函数。
6.已知![]() 的最大值为a,最小值为b,
的最大值为a,最小值为b,![]() 的最大值为c,最小值为d,则有
的最大值为c,最小值为d,则有
A、b<d<a<c B、d<b<c<a C、b<d<c<a D、d<b<a<c
7.已知![]() 为偶函数,求
为偶函数,求![]() 的值。
的值。
8.已知函数![]() ;(1)求它的定义域,值域;
;(1)求它的定义域,值域;
(2)指出它的单调区调;(3)判断它的奇偶性;
(4)判断它的周期性,如果是周期函数,求出它的一个周期。
4.9函数![]() 的图象(3课时)
的图象(3课时)
第一课时 图象变换
1.求函数![]() 的最小正周期。
的最小正周期。
2.要得到函数![]() 的图象只需将
的图象只需将![]() 的图象( )
的图象( )
A、向左平移![]() 个单位 B、向右平移
个单位 B、向右平移![]() 个单位
个单位
C、向左平移![]() 个单位 D、向右平移
个单位 D、向右平移![]() 个单位
个单位
3.![]() 的对称轴为
,对称中心为
。
的对称轴为
,对称中心为
。
4.如何变换![]() 的图象得到函数
的图象得到函数![]() 的图象?
的图象?
5.如何由![]() 的图象得到
的图象得到![]() 。
。
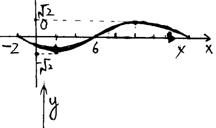
6.如图为![]() 的图象的一段,确定其解析式。
的图象的一段,确定其解析式。
![]()
第二课时 巩固图象变换并推广到一般函数
1.函数![]() 在区间
在区间![]() 上是增函数;且
上是增函数;且![]() 则函数
则函数![]() 在
在![]() 上( )
上( )
A、是增函数 B、是减函数
C、可以取得最大值M
D、可以取得最小值![]()
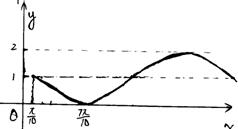 2.函数
2.函数![]() 的图象如右图所示,则
的图象如右图所示,则![]() 解析式为( )
解析式为( )
A、![]()
B、![]()
C、![]()
D、![]()
3.已知函数![]() 若将
若将![]() 的图象上的每个点的横标保持不变,纵标扩大为原来的2倍,然后再将整个图象向下平移1个单位,得到曲线与
的图象上的每个点的横标保持不变,纵标扩大为原来的2倍,然后再将整个图象向下平移1个单位,得到曲线与![]() 的图象相同,则
的图象相同,则![]() 的解析式是( )
的解析式是( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
4.把函数![]() 的图象向左平移m个单位,所得的图象关于
的图象向左平移m个单位,所得的图象关于![]() 轴对称,则m的最小值为( )
轴对称,则m的最小值为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
5.函数![]() 有下列命题:
有下列命题:
①由![]() 可得
可得![]() 必是
必是![]() 的整数倍;
的整数倍;
②![]() 的表达式可改写成
的表达式可改写成![]() ;
;
③![]() 的图象关于点
的图象关于点![]() 对称;
对称;
④![]() 的图象关于直线
的图象关于直线![]() 对称;
对称;
⑤在区间![]() 上是增函数。
上是增函数。
写出你认为正确的论断有 (所有的。)
6.若函数![]() 且
且![]() ,
,
(1)求函数![]() 的解析式;
的解析式;
(2)用“五点法”作出![]() 在一个周期内的图象;
在一个周期内的图象;
(3)讨论函数![]() 的性质。(定义域、值域、奇偶性、最小正周期、单调性)
的性质。(定义域、值域、奇偶性、最小正周期、单调性)
第三课时:![]() 图象与物理的联系
图象与物理的联系
1.已知函数![]() 的最小值为
的最小值为![]() ,周期为
,周期为![]() 且图象过点
且图象过点![]() ,求此函数的解析式。
,求此函数的解析式。
2.设![]() 最高点D的坐标
最高点D的坐标![]() ,由最高点运动到相邻的最低点F时,曲线与x轴交于E(6,0)。
,由最高点运动到相邻的最低点F时,曲线与x轴交于E(6,0)。
(1)求![]() 之值;
之值;
(2)确定函数![]() 的表达式,使图象与
的表达式,使图象与![]() 的图象关于直线
的图象关于直线![]() 对称
对称
3.已知函数![]() (其中A、B、
(其中A、B、![]() 是实常数,且
是实常数,且![]() )的最小正周期为2,并当
)的最小正周期为2,并当![]() 时,
时,![]() 的取得最大值2。求函数
的取得最大值2。求函数![]() 的表达式;
的表达式;
4.函数![]() ,
,
(1)当函数![]() 取得最大值时,求自变量
取得最大值时,求自变量![]() 的集合。
的集合。
(2)该函数的图象可由![]() 的图象经过怎样的平移和伸缩变换得到?
的图象经过怎样的平移和伸缩变换得到?
5.![]() 的振幅是
,频率是
,平衡位置是
。
的振幅是
,频率是
,平衡位置是
。
4.10正切函数的图象与性质(两课时)
第一课时:正切函数的图象和性质
1.根据正切函数的图象写出下列不等式的解集
①![]() ;
②
;
②![]()
2.求下列函数的定义域:
①![]() ②
②![]()
3.求函数![]() 的定义域和值域。
的定义域和值域。
4.满足![]() 的角
的角![]() 的一个取值区间是( )
的一个取值区间是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
5.![]() 的定义域是
。
的定义域是
。
6.在区间![]() 范围内,函数
范围内,函数![]() 与函数
与函数![]() 的图象交点的个数为( )
的图象交点的个数为( )
A、1 B、2 C、3 D、4
7.若![]() 则下列关系式中成立的是( )
则下列关系式中成立的是( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
8.作出![]() 在
在![]() 内图象,并求出定义域和值域。
内图象,并求出定义域和值域。
第二课时:图象变换与性质
1.由![]() 知,余切函数的定义域为
,其图象可由正切函数
知,余切函数的定义域为
,其图象可由正切函数![]() 的图象先将所有点向
平移
个单位,再将所得图象绕
翻转1800而得到。
的图象先将所有点向
平移
个单位,再将所得图象绕
翻转1800而得到。
2.![]() 图象
轴对称图形(填是或不是),
中心对称图形,若是分别为
。
图象
轴对称图形(填是或不是),
中心对称图形,若是分别为
。
3.求![]() 的对称中心。
的对称中心。
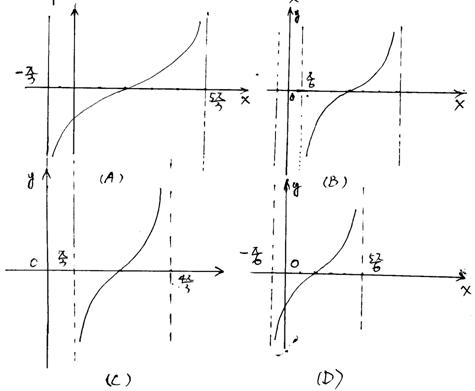
4.函数![]() 在一个周期内的图象是( )
在一个周期内的图象是( )
5.函数![]() 的单减区间是
。
的单减区间是
。
6.![]() 的对称中心为
。
的对称中心为
。
4.11已知三角函数值求角(两课时)
第一课时:知值求角
1.分别求满足下列条件的![]() ABC的内角A:
ABC的内角A:
①![]() ;②
;②![]() ; ③
; ③![]() ;④
;④![]()
2.根据下列条件求![]() 内的角
内的角![]() 。
。
①![]() ;②
;②![]() ;③
;③![]() 。
。
3.已知:![]() 求
求![]() 的集合。
的集合。
4.已知:![]() 求
求![]() 的集合。
的集合。
5.已知:![]() 求
求![]() 的集合。
的集合。
第二课时,反三角
1.已知![]() 求
求![]() 的集合。
的集合。
2.已知![]() ,则
,则![]() =
。
=
。
3.已知![]() ,则
,则![]() =
。
=
。
4.![]() 。
。
5.![]() =
。
=
。
6.满足条件![]() 的
的![]() 值是( )
值是( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
7.已知![]() ,且
,且![]() ,求角
,求角![]() 。
。
8.已知![]() ,求
,求![]() 的值。(用反三角函数表示)
的值。(用反三角函数表示)
4.8正弦、余弦函数的图象和性质参考答案
课时1
1.画出下列函数的图象。
课时2
1.①要使函数有意义,须满足![]() 即
即![]() 。由正弦曲线知:
。由正弦曲线知:
![]() 即原函数定义域为
即原函数定义域为![]()
设![]() 由
由![]() 知:
知:![]()
![]()
即原函数值域为![]() 。
。
2.解:将原函数解析式变形为:![]()
![]() 否则无意义,
否则无意义,![]()