专题一 立体几何
班级： _____ 姓名： _____ 学号： _____
一、选择题(4分×10=40分)
1．直线
和
，
，
与
平行，则
与
的关系是
A．平行 B．相交 C．垂直 D．以上都可能
2．若线段AB的长等于它在平面内射影长的3倍，则这条斜线与平面所成角的余弦值为
A．
B． 
C．
D．
3．在正方体ABCD-A1B1C1D1中，B1C与平面DD1B1B所成的角的大小为
A．
B．
C．
D．
4．有下列命题：①空间四点共面，则其中必有三点共线；②空间四点不共面，则其中任何三点不共线；③空间四点中有三点共线，则此四点共面；④空间四点中任何三点不共线，则此四点不共面．其中正确的命题是
A．②③ B．①②③ C．①③ D．②③④
5．有一山坡，倾斜度为300，若在斜坡平面上沿着一条与斜坡底线成450角的直线前进1公里，则升高了
A．
米 B． 
米 C．
米 D． 500米
6．已知三条直线
及平面
，则下列命题中正确的是
A．
B．若
，则
C． 若
，则
D．若
则
7．已知P是△EFG所在平面外一点，且PE=PG，则点P在平面EFG内的射影一定在△EFG的
A．∠FEG的平分线上 B．边EG的垂直平分线上
C．边EG的中线上 D．边EG的高上
8．若一正四面体的体积是
cm3，则该四面体的棱长是
A． 6cm B． 
cm C．12cm D．
cm
9．P是△ABC所在平面α外一点，PA，PB，PC与α所成的角都相等，且PA⊥BC，则
△ABC是
A．等边三角形 B．直角三角形 C．等腰三角形 D．等腰直角三角形
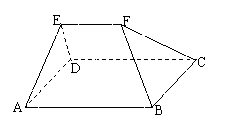10．如图，在多面体ABCDEF中，已知ABCD是边长为3的正方形，EF//AB，EF=
，EF与面AC的距离为2，则该多面体的体积为
A．2 B．4 C．
D．
二、填空题(4分×4=16分)
11．空间四边形ABCD中，AB=6，CD=8，E、F、G分别是BD，AC，BC的中点，若异面直线AB和CD成600的角，则EF= 。
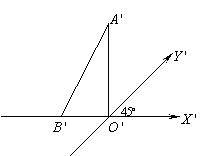
12．如图， 
表示水平放置的
的直观图，
在
轴上，
和轴垂直，且
．则的边
上的高为_______
_________________________
13．已知正四棱台的上、下底面边长分别为4和10，侧棱长为5．它的主视图和左视图是两个全等的等腰梯形，则该等腰梯形的面积为_________________________________
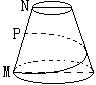
14．如图，已知圆台的上、下底面半径分别为1cm，3cm，母线长为8cm，P是母线MN的中点，由M出发，沿圆台侧面绕一周到达点P，则经过的最短路程为 。
一、选择题 (每小题4分共40分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
二、填空题: (每小题4分共16分)
11．_________________________ 12．_________________________
13．_________________________ 14．_________________________
三、解答题(10分+12分+10分+12分=44分)
15．一个正方体的顶点都在球面上，它的棱长等于2cm．
（１）求这个外接球的表面积和体积；
（２）求这个正方体的内切球的表面积和体积．
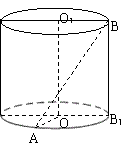
16．如图，OO1为圆柱的轴，Ａ，Ｂ分别为两底面圆周上的点，且OA⊥OB．
（１）判断OO1与底面的位置关系，并证明你的结论；
（２）若为BB1圆柱的母线，求证：平面ABB1垂直于圆柱的底面；
（３）若圆柱的轴截面是一个正方形，求异面直线AB与OO1所成角的正切值．
 |
17．如图，ABCD是边长为2a的正方形，PB⊥平面ABCD，MA
PB，且PB=2MA=2a，E是PD中点．
(1) 
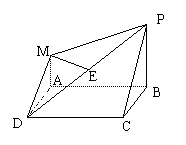求证：ME平面ABCD； (2) 求点B到平面PMD的距离．
18．如图１为等腰梯形PDCB，DC=1，PB=3，DA为底边PB上的高，垂足为A，且AD=1．
现将等腰梯形PDCB沿DA折成直二面角P﹣AD﹣B，如图２．
（１）求四棱锥P﹣ABCD的体积；
（2）求二面角
的余弦值；
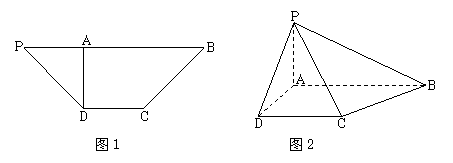（3）求证：平面PAC⊥平面PBC．