第一课时 3.2.1简单的三角恒等变换
教学重点：引导学生以已有的十一个公式为依据，以推导积化和差，和差化积，半角公式为基本训练，学习三角变换的内容，思路和方法，在与代数变换相比较中，体会三角变换的特点，提高推理，运算的能力。
教学难点：认识三角变换的特点，并能运用数学思想方法推导变换过程的设计，不断提高从整体上把握变换过程的能力。
教学过程：
一. 复习准备
1. 提问：前面学过的倍角公式是什么？（学生说，老师板书）
2.
讨论：
与
有什么关系？（学生回答）
二.讲授新课
1.通过讨论知道，是的二倍角，在复习的倍角公式中，让学生以代替
，以代替
将公式进行改写。（可以请两个学生板演，老师巡查整个教室，最后师生一起检查板演的作业）
2.出示例1：老师将刚才的结果进行改写，即半角公式。
3.讨论：代数式的变换与三角变换有什么不同？
结论：代数式变换着眼于式子结构形式的变换；三角变换首先寻找式子所包含的各个角之间的联系，并以此为依据选择可以联系它们的适当公式，这是三角式恒等变换的重要特点。
4.出示例2
讨论：这两个式子的左右两边在结构形式上有什么不同？
（如果记
，则有
。只要解上述方程组，就可以求出
，即求出
）
结论：把两个三角式结构形式上的不同点作为思考的出发点，并在建立它们之间的联系进而消除不同点上下功夫，这样不仅有利于深化对和（差）角公式的理解，而且还有利于这两题内在联系的认识。
5.练习：1）求证
2）求证
（学生板演，老师讲解）
6.小结：做证明题，要分析题意，明确思维起点；选择公式，把握思维方向；实施变换，运用数学思想方法
三.巩固练习：
1.教材P155练习2，3题
2.作业：P156 习题1中（2）（3）
第二课时 3.2.2简单的三角恒等变换
教学重点：更进一步理解三角恒等变换的内容，思路和方法， 熟练的进行三角恒等变换的应用
教学难点：三角恒等变换的应用
教学过程：
二. 复习准备：
1.提问： 
的周期？最大值？最小值？（学生回答，老师板书）
2.提问：两角和与差的正弦和余弦公式？（学生回答，老师板书）
二.讲授新课
1.讨论函数
的周期，最大值，最小值？
（学生回答，老师点评）
2.练习：
(学生板演，老师评讲)
3.总结：对一般的
，周期，最大值，最小值？（教师给出）
4.练习: 求周期和最值：
（师生共练）
5.出示P154例4：学生讲思路，老师点评，然后师生一起写过程
对于例4 ，还可以去掉“记
”，结论改写成“求矩形
的最大面积”
这时，在建立函数模型时，对自变量可多一种选择，如设
，则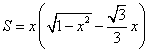
三.巩固练习：
1.已知函数
（1）求它的递减区间；（2）求它的最大值和最小值2.已知函数
（1）求它的最小正周期
（2）当
时，求它的最小值以及取得最小值时自变量的集合。
四.课堂总结
通过三角变换，我们把形如的函数转化为形如的函数，从而使问题得到简化，这个过程中蕴涵了化归思想。
作业：P157 A组 5
P160A组10
第三章小结
一．教学重点
引导学生通过独立探索和讨论交流，导出两角和与差的三角函数的十一个公式，并了解它们的内在联系；同时引导学生以已有的十一个公式为依据，以推导积化和差，和差化积 ，半角公式作为基本训练，学习三角变换的内容，思路和方法，在与代数变换相比较中，体会三角变换的特点，提高推理和运算能力。
二．教学难点
两角差的余弦公式的探索和证明；认识三角变换的特点，并能运用数学思想方法指导变换过程的设计，不断提高从整体上把握变换过程的能力。
三．教学过程
1.本章知识结构框图
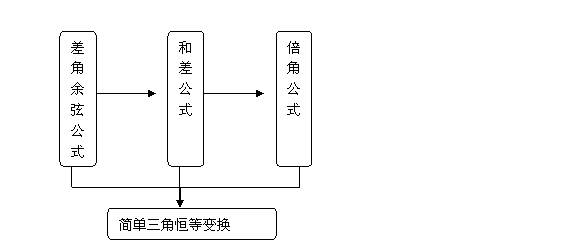
2.例题讲解
1.已知
，求
值。
2.已知
，
，求
值。
| |
在区间
上的最大值是6，求常数
的值及此函数当
时的最小值，并求相应的的取值集合
4.如图，正方形ABCD的边长为1 ，P，Q分别为
边AB，DA上的点。当
的周长为2时，求
的大小。
3.巩固练习
1.已知
，求
值。
2.已知
，
，求
值