第一课时 3.1.1两角差的余弦公式（一）
教学要求：经历用向量的数量积推导出两角差的余弦公式的过程，进一步体会向量方法的作用
教学重点：用向量的数量积推导出两角差的余弦公式
教学难点：两角差的余弦公式的推导及运用
教学过程：
一、复习准备：
1. 向量的知识：数量积
;
二、讲授新课：
1. 新课导入：①情景导入：我们在初中时就知道 
，
，由此我们能否得到
大家可以猜想，是不是等于
呢？
根据第一章所学的知识可知猜想是错误的！下面一起探讨两角差的余弦公式
在第一章三角函数的学习当中我们知道，在设角
的终边与单位圆的交点为
，
等于角与单位圆交点的横坐标，也可以用角的余弦线来表示，大家思考：怎样构造角
和角
？（注意：要与它们的正弦线、余弦线联系起来.）
思考：我们在第二章学习用向量的知识解决相关的几何问题，两角差余弦公式我们能否用向量的知识来证明？
提示：1、结合图形，明确应该选择哪几个向量，它们是怎样表示的？
2、怎样利用向量的数量积的概念的计算公式得到探索结果？
2.教学：
记忆：右端为
的同名三角函数积的和左端为两角差的余弦
例1、利用余弦公式计算
的值
点评：把一个具体角构造成两个角的和、差形式，有很多种构造方法，要学会灵活运用.
例2、已知
，
是第三象限角，求
的值.
点评：注意角、的象限，也就是符号问题.
3.小结：学习两角差的余弦公式，首先要认识公式结构的特征，了解推导过程，熟知由此衍变的两角和的余弦公式.在解题过程中注意角、的象限，也就是符号问题，学会灵活运用.
三、巩固练习：
1. 已知
2. 
3. 
作业：课本第150页第2、3、4题
第二课时 3.1.2 两角和与差的正弦、余弦、正切公式
教学要求：理解以两角差的余弦公式为基础，推导两角和、差正弦和正切公式的方法，体会三角恒等变换特点的过程，理解推导过程，掌握其应用.
教学重点：两角和、差正弦和正切公式的推导过程及运用
教学难点：两角和与差正弦、余弦和正切公式的灵活运用
教学过程：
一、复习准备：
1. ，讨论当为
时呢？
再利用两角差的余弦公式得出
二、讲授新课：
1. 新课教学：
思考两角和与差的正弦公式是怎样的呢？提示：在第一章我们用诱导公式五（或六）可以实现正弦、余弦的互化，这对我们解决今天的问题有帮助吗？让学生动手完成两角和与差的正弦、正切公式.
．
让学生观察认识两角和与差正弦公式的特征，并思考两角和与差正切公式.（学生动手）
．
通过什么途径可以把上面的式子化成只含有
、
的形式呢？
以上我们得到两角和的正切公式，我们能否推导出两角差的正切公式呢？
2.例题教学：
例1、已知
是第四象限角，求
的值.
例2、利用和（差）角公式计算下列各式的值：
（1）
；（2）
；（3）
分析：解此类题首先要学会观察，看题目当中所给的式子与我们所学的两角和与差正弦、余弦和正切公式中哪个相象.
3. 小结：本节我们学习了两角和与差正弦、余弦和正切公式，我们要熟记公式，在解题过程中要善于发现规律，学会灵活运用
三、巩固练习：
1.化简
2.已知
求
的值．（
）
3.已知
，求
的值．
第三课时 二倍角的正弦、余弦和正切公式
教学要求：以两角和正弦、余弦和正切公式为基础，推导二倍角正弦、余弦和正切公式，理解推导过程，了解它们的内在联系，并能运用上述公式进行简单的恒等变换.
教学重点：以两角和的正弦、余弦和正切公式为基础，推导二倍角正弦、余弦和正切公式
教学难点：二倍角的理解及其灵活运用
教学过程：
一、复习准备：
大家首先回顾一下两角和的正弦、余弦和正切公式，
；
；
．
思考：当
=
这些公式会变成怎么样呢？
二、讲授新课：
1. 新课教学：
；
；
思考：把上述关于
的式子能否化为只含有
或形式的式子吗？
；
．
2. 例题教学：
例1、已知
求
的值．
例２、已知
求的值．
解：
，由此得
解得
或
例3.① 化简
；②求
的值
3. 小结：本节我们学习了二倍角的正弦、余弦和正切公式，我们要熟记公式，在解题过程中要善于发现规律，学会灵活运用.
三、巩固练习：
1. 练习：求证
2. 变式：化简
3.求证
4.化简：
作业：课本150页11题，14题，15题
第四课时 两角和与差的正弦、余弦、正切（综合练习）
教学要求：以两角和正弦、余弦和正切公式为基础，推导二倍角正弦、余弦和正切公式，理解推导过程，掌握其应用
教学重点：公式的理解及熟练运用、灵活运用
教学难点：公式的理解及其灵活运用
教学过程：
一、复习准备：
首先回顾两角和的正弦、余弦和正切公式，
；
；
．
；
；
； 
二、讲授新课：
1. 教学：
⑴例题：
已知一元二次方程
的两个根为
，求
的值；
变式：求
的值.说明：虽然是方程的两个根，但我们并不需要求出
⑵求值：
（1）
；（2）
⑶求角度:
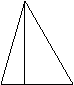
如图，在△ABC中，AD⊥BC，垂足为D，且BD：DC：AD=2：3：6，求∠BAC的度数.
⑷求三角函数最值：
已知函数
当函数
取得最大值时，求自变量
的集合.
2.小结：
在本小节的公式中，两角和与差的正弦、余弦公式是基础，特别是两角和的余弦公式，它几乎是这一章的中心公式，我们今后要学的其他三角公式，全部可以由它推导，甚至是诱导公式。要记住、熟练运用这些公式只有一个办法：多作题目，从做题中找感觉，感觉是从做题中得出的.
三、巩固练习：
1.在△ABC中，已知
, 
，求
的值.
2.已知
，求
的值.
3.已知
，求
的值.
4．求
作业：课本：第151页17、18题