第一课时 2.1 平面向量的实际背景及基本概念(一)
教学要求: 理解向量、零向量、单位向量、平行向量的概念：掌握向量的几何表示，会用字母表示向量.
教学重点：向量、零向量、单位向量、平行向量的概念.
教学难点：向量及相关概念的理解，零向量、单位向量、平行向量的判断.
教学过程：
一、复习准备：
1. 讨论： 到目前为止我们物理学习中学过时间、温度、位移、质量、体积、力等. 哪些是既有大小又有方向？哪些只有大小而没有方向？
2．如何定义有向线段？
3. 三角函数线有没有大小和方向？是否可用有向线段表示？
二、讲授新课：
1. 教学向量的概念：
① 定义向量：既有大小又有方向的量.
练习：时间、温度、位移、质量、体积、力，哪些是向量？
②讨论：数量与向量有何区别？向量是否可以比较大小？
（数量只有大小，可以比较大小. 向量不可以比较大小）
③
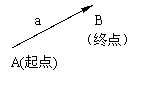
定义有向线段：带有方向的线段叫有向线段. 记作
，以A为起点，B为终点，几何表示时在其终点处画上箭头表示方向. （如图）
有向线段的三要素：起点、方向、长度.
④ 向量的表示：向量可以用有向线段表示，记作；也可以用字母表示，如：
.
⑤ 定义模：向量的大小（长度）叫向量的模，记作
，
⑥ 练习：画出一向正东方向以20m/s的速度行驶的小车的速度.
⑦ 定义零向量：长度为0的向量，记作
，规定零向量的方向可以为任意方向.
⑧ 定义单位向量:长度为1个单位长度和向量叫单位向量.
⑨ 讨论：单位向量是否唯一？有多少个单位向量？
2．教学例题：
① 例：温度有零上零下之分，“温度”是否向量？
答：不是. 因为零上零下也只是大小之分.
② 出示课本例题：84页例1. （师生共同完成：确定起点、方向、长度. 特别注意方向）
练习：在方格图中画出20N竖直向上和15N向正左方向的力.
③ 定义平行向量：方向相同或相反的两向量叫平行向量，记作：
∥
.
规定零向量平行于任何去何从向量.
3．小结：向量的定义，向量由其大小与方向确定. 向量不可比较大小但其模可以比较大小.
三、巩固练习：
1．判断下列式子是否正确，若不正确请指出错误原因.
① 
=0 ② .-=0
2．若将所有单位向量的起点归结在同一起点，则其终点构成的图形是------------------.
3．在正方形ABCD中试找出有哪几对向量是平行向量.
4．回答下列问题：
①平行向量是否一定方向相同？
②与任何向量都平行的向量是什么向量？
5. 作业：课本86页习题A组1、2题.
第二课时 2.1 平面向量的实际背景及基本概念(二)
教学要求：掌握相等向量、共线向量的概念，会判断共线向量与相等向量.
教学重点：判断共线向量与相等向量
教学难点: 相等向量、共线向量的概念
教学过程：
一、复习准备：
1. 有向线段的三要素是什么?
2．如何定义向量，怎样表示向量？（用有向线段或字母表示）
3. 什么是零向量、单位向量？零向量有何特点？
4. 试讨论：平行向量通过平移后是否可以移至同一直线上？
二、讲授新课：
1. 教学相等向量与共线向量的概念：
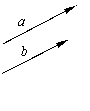
① 定义共线向量：任一组平行向量都可移到同一条直线上 ，所以平行向量也叫共线向量.
② 定义相等向量：长度相等且方向相同的向量叫做相等向量.
记作：=
规定：=
2.教学例题：
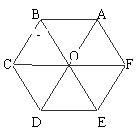
① 例１如图，设Ｏ是正六边形ＡＢＣＤＥＦ中心，分别写出图中与
向量
相等的向量,与向量
平行的向量.
（先师生共同完成，紧扣定义）
② 变式训练：
变式一：与向量
长度相等的向量有多少个？（11个）
变式二：是否存在与向量长度相等、方向相反的向量？
变式三：与向量
共线的向量有哪些？（
）
3．小结：相等到向量、共线向量.
三、巩固与提高：
1． 将所有共线向量移至同一起点，终点构成的图形是什么图形？
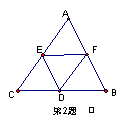
2．
如图
分别是
的三边
的中点,写出与向量
共线的向量
3．下列说法正确的是（ ）
A. 平行向量是方向相同的向量 B. 零向量的长度为0
C. 长度相等的向量叫相等向量 D. 共线向量是在同一条直线上的向量
4．若非零向量与共线，则以下说法下确的是（ ）
A. 与必须在同一直线上 B. 与平行，且方向必须相同`
C. 与平行，且方向必须相反 D. 与平行
5．作业：86页A组第5题.