第一课时 2.4.1 平面向量的数量积的物理背景及其含义
教学要求：掌握平面向量的数量积及其几何意义；掌握平面向量数量积的重要性质及运算律；了解用平面向量的数量积可以处理有关长度、角度和垂直的问题；
教学重点：平面向量的数量积定义及应用.
教学难点：平面向量数量积的定义及运算律的理解.
教学过程：
一、复习准备：
1. 如何由坐标得到两个向量共线?
2. 物理中力做的功是怎样定义的？
二、讲授新课：
1.教学向量的数量积的概念.
①.两个非零向量夹角的概念：已知非零向量ａ与ｂ，作
＝ａ，
＝ｂ，则∠ＡＯＢ＝θ（０≤θ≤π）叫ａ与ｂ的夹角.注意：当θ＝０时ａ与ｂ同向；当θ＝π时，ａ与ｂ反向；当θ＝
时，ａ与ｂ垂直，记ａ⊥ｂ；
②.平面向量数量积（内积）的定义: 已知两个非零向量ａ与ｂ，它们的夹角是θ，则数量abcosq叫ａ与ｂ的数量积，记作a×b，即有a×b = abcosq，
（分析：符号由cosq的符号所决定；两个向量的数量积称为内积，写成a×b；）
③.“投影”的概念：作图定义：bcosq叫做向量b在a方向上的投影. 投影也是一个数量，不是向量；当q为锐角时投影为正值；当q为钝角时投影为负值；当q为直角时投影为0；当q = 0°时投影为 b；当q = 180°时投影为 -b
④．向量的数量积的几何意义：数量积a×b等于a的长度与b在a方向上投影bcosq的乘积.
⑤.性质：e×a = a×e =acosq ，a^b Û a×b = 0，当a与b同向时，a×b = ab；当a与b反向时，a×b = -ab. 特别的a×a = a2或
cosq =
）
⑥探究：运算律 a×b=b.a (λa).b=λ(a.b)
2.教学例题
①.讲解范例：例1 已知a=5， b=4， a与b的夹角θ=120o，求a·b.
例2 已知a=6， b=4， a与b的夹角为60o求(a+2b)·(a-3b).
例3 已知a=3， b=4， 且a与b不共线，k为何值时，向量a+kb与a-kb互相垂直.
（教师演示
学生模仿学生演示）
②.练习：已知｜ａ｜＝３，｜ｂ｜＝６，当①ａ∥ｂ，②ａ⊥ｂ，③ａ与ｂ的夹角是60°时，分别求ａ·ｂ.
3. 小结：1.平面向量数量积（内积）的定义；2.向量的数量积的几何意义.
三、巩固练习：
1．已知a=1，b=
，(1)若a∥b，求a·b；(2)若a、b的夹角为６０°，求a+b；(3)若a-b与a垂直，求a与b的夹角.
2．设m、n是两个单位向量，其夹角为６０°，求向量a=2m+n与b=2n-3m的夹角.
3．对于两个非零向量a、b，求使a+tb最小时的t值，并求此时b与a+tb的夹角.
4．已知a+b=2i-8j，a-b=-8i+16j，其中i、j是直角坐标系中x轴、y轴正方向上的单位向量，那么a·b=？
5.作业：课本P119 A组 1，2，3题.
第二课时 2.4.2平面向量数量积的坐标表示、模、夹角
教学要求：使学生掌握平面向量数量积的坐标表示, 掌握向量垂直的坐标表示的条件，及平面内两点间的距离公式,能用所学知识解决有关综合问题.
教学重点：平面向量数量积的坐标表示的应用.
教学难点：平面向量数量积的坐标表示的综合运用
教学过程：
一、复习准备：
1.平面向量的数量积的物理背景及其含义?
2.向量的数量积的几何意义.
3.平面向量数量积的运算律.
二、讲授新课：
1．教学坐标表示.
① 平面两向量数量积的坐标表示: 两个向量的数量积等于它们对应坐标的乘积的和.即
② 平面内两点间的距离公式: 如果表示向量
的有向线段的起点和终点的坐标分别为
、
，那么
③ 向量垂直的判定: 设
，
，则
④ 两向量夹角的余弦（
） cosq =
2．教学例题.
① 讲解例5：已知A(1， 2)，B(2， 3)，C(-2， 5)，试判断△ABC的形状，并给出证明
练习：在△ABC中，
=(2，
3)，
=(1， k)，且△ABC的一个内角为直角，求k值.
（学生板演→教师修正→学生修正）
② 讲解例6：设= (5， -7)，
= (-6， -4)，求a·b及、间的夹角θ(精确到1o)
练习：已知A(1，0)，B(3，1)，C(2，0)，且=
，=
，则与的夹角为多少？
（学生板演→教师修正→学生修正）
3．小结： 平面内两点间的距离公式；向量垂直的判定；两向量夹角的余弦.
三、巩固练习：
1．已知A(3，2)，B(-1，-1)，若点P(x，-
)在线段AB的中垂线上，则x= .
2．=(2，3)，=(-2，4)，则(+)·(-)= .
3. 已知A(1，2)，B(2，3)，C(-2，5)，则△ABC为（ ）
A.直角三角形 B.锐角三角形 C.钝角三角形 D.不等边三角形
4. 已知＝（１，
），＝（＋１，－１），则与的夹角是多少?
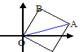5. 如图，以原点和A(5， 2)为顶点作等腰直角△OAB，使ÐB = 90°，求点B和向量的坐标.
6. 已知 (4,2), 求与垂直的单位向量的坐标.
7. 作业：课本P119 练习（1）（2）