第一课时 2.2. 1 向量的加(减)法运算及其几何意义
教学要求:掌握向量的加法与减法的意义与几何运算,会运用三角形法则、平行四边形法则进行向量的加(减)法运算
教学重点:运用三角形法则、平行四边形法则运算
教学难点:向量加法、减法的几何意义
 教学过程:
教学过程:
一、复习准备:
1. 如何定义相等向量和共线向量?
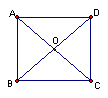
2.如图:![]() 是正方形
是正方形![]() 的中心,①向量
的中心,①向量![]() 与
与![]() 相等吗?
相等吗?
② 向量![]() 与
与![]() 是平行向量吗? ③ 求
是平行向量吗? ③ 求![]() :
:![]() 的值.
的值.
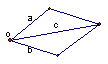 3.回顾思考:力是向量,如何求
3.回顾思考:力是向量,如何求![]() 、
、![]() 这两个力的合力呢?用什么方法?
这两个力的合力呢?用什么方法?
二、讲授新课:
1. 教学向量的加(减)法运算:
① 向量的加(减)法:求两向量和(差)的运算叫向量的加(减)法运算
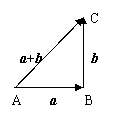 ② 三角形法则:向量
② 三角形法则:向量![]() 与
与![]() 相加时,
相加时,![]() 的终点B作为
的终点B作为![]() 的起点,这时起点A到终点C的向量
的起点,这时起点A到终点C的向量![]() 就是这两个向量的和向量,即
就是这两个向量的和向量,即
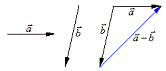
![]() . 这种求向量和的方法叫三角形法则. (
. 这种求向量和的方法叫三角形法则. (![]() )
)
(注意:两个向量要“首尾”相接)
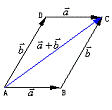 ③平行四边形法则:由同一点A为起点的两个已知向量
③平行四边形法则:由同一点A为起点的两个已知向量![]() 为邻边作平行四边形ABCD,则以A为起点的向量
为邻边作平行四边形ABCD,则以A为起点的向量![]() 就是向量
就是向量![]() 的和. 这种作两个向量和的方法叫做平行四边形法则,如右图:
的和. 这种作两个向量和的方法叫做平行四边形法则,如右图:
④讨论:三角形法则、平行四边形法则是否对所有向量![]() 求和都适用?
求和都适用?
(注意:平行四边形法则对于两个向量共线时不适用. )
⑤定义相反向量:与向量![]() 的长度相等、方向相反的向量叫做向量
的长度相等、方向相反的向量叫做向量![]() 的相反向量,记作:
的相反向量,记作:![]()
规定零向量的相反向量仍是零向量.
注:向量![]() 可以看成是
可以看成是![]()
2. 教学例题:
① 课本![]() 例1、
例1、![]() 例3,
例3,![]() 例4.
例4.
(师生共同完成,注意两种法则的区别,然后变式——加变减、减变加)
② 练习:课本93页第1、2题.
③ 讨论:![]() 与
与![]() 、
、![]() 与
与![]() 有何关系.
有何关系.
④ 用三角形法则、平行四边形法则探讨向量的加减运算是否满足交换律、结合律.
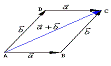
 ⑤
⑤ ![]() 例2. (向量的实际应用,师生共同完成;变式:若船行走的路线是垂直于河岸,求速度)
例2. (向量的实际应用,师生共同完成;变式:若船行走的路线是垂直于河岸,求速度)
三、巩固练习:
1.如右图,画出![]() .
.
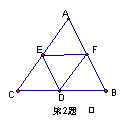
2.如图,D、E、F分别为三边的中点,试画出![]() -
-![]() 、
、![]() 、
、![]()
3.作业:93页第1、2题.
第二课时 2.2. 3 向量数乘运算及其几何意义
教学要求:理解向量的数乘运算及其几何意义,会进行向量的数乘运算.
教学重点:向量的数乘运算
教学难点:向量的数乘运算的几何意义
教学过程:
 一、复习准备:
一、复习准备:
1. ![]() 与
与![]() 、
、![]() 与
与![]() 有何关系?什么时候等号成立?
有何关系?什么时候等号成立?
2.如图:![]() 是正方形
是正方形![]() 的中心,求下列各式的值
的中心,求下列各式的值
①![]() +
+![]() ②
② ![]() -
-![]()
3.![]() 为非零向量,试求
为非零向量,试求![]() 和
和![]() 的值.
的值.
二、讲授新课:
1. 教学向量的数乘运算:
①
向量的数乘:求实数![]() 与向量
与向量![]() 的乘积的运算叫向量的数乘,记作:
的乘积的运算叫向量的数乘,记作:![]()
规定:(Ⅰ) ![]() 仍然是个向量
(Ⅱ)、
仍然是个向量
(Ⅱ)、![]()
(Ⅲ) 当![]() 时向量
时向量![]() 的方向与
的方向与![]() 的方向相同,当
的方向相同,当![]() 时,向量
时,向量![]() 与
与![]() 的方向相反,
的方向相反,
当![]() 时,
时,![]()
② 练习:![]() 为单位向量,试求
为单位向量,试求![]() 、
、![]() 、
、![]() 、
、![]() 的值:变式:
的值:变式:![]() 为非零向量.
为非零向量.
③ 讨论验证下列等式:![]() 、
、![]() 为实数,
为实数,![]() 、
、![]() 为向量.
为向量.
⑴ ![]() ⑵
⑵ ![]() ⑶
⑶ ![]()
(数乘运算满足交换律、结合律、分配律)
2、教学例题:
① 例5:计算:⑴![]() ⑵
⑵ ![]() ⑶
⑶![]()
(去括号,实数与实数运算后再与向量运算)
② 定理:向量![]() 与
与![]() 共线(
共线(![]() ),当且仅当有唯一一个实数
),当且仅当有唯一一个实数![]() ,使
,使![]() .
.
 ③ 出示例题6:(分析:三点可分共线与不共线两种情形,可以通过判断以这三点为端点的向 量是否共线来判断点是否共线)
③ 出示例题6:(分析:三点可分共线与不共线两种情形,可以通过判断以这三点为端点的向 量是否共线来判断点是否共线)
④ 定义线性运算:向量的加、减、数乘运算统称为向量的线性运算.
⑤ 出示例题7. (先找出与![]() 、
、![]() 向量共线的向量,再利用定理)
向量共线的向量,再利用定理)
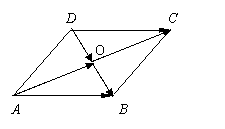
⑥ 练习:如图,试用向量方法证明:对角线互相平分的四
边形是平行四边形
3.小结:向量的数乘运算;两向量![]() 与
与![]() 共线满足
共线满足![]()
三、巩固练习
1. 计算:(1)![]() (2)
(2)![]()
2. 已知向量,求作向量![]() ,使
,使![]() ,表示的有向线段能构成三角形吗?
,表示的有向线段能构成三角形吗?
3.求证:M是线段AB的中点,对于任意一点O,都有![]()
4.在三角形ABC中,![]() ,
,![]() ∥
∥![]() 交AC于F点,试用
交AC于F点,试用![]() 、
、![]() 表示
表示![]() .
.
5.作业:课本第100页第4、5题.
第三课时 2.2. 3 向量的相关概念及向量线性运算(练习)
教学要求:掌握向量的相关概念,能熟练进行向量的线性运算.
教学重点:向量的线性运算,掌握向量运算的几何作图.
教学难点:向量的线性运算.
教学过程:
一、相关概念:
1. 回顾向量、零向量、单位向量、平行向量、、共线向量、相反向量相等向量是如何定义的.
(是否是零向量、单位向量只需判断长度,要判断是否为相等向量、共线向量、相反向量则还要看方向)
2.向量的加、减、数乘运算统称为向量的线性运算.
3.要判断两向量是否共线,只需证明![]()
![]() .
.
4.回答下列问题:
① 平行向量是否一定方向相同?
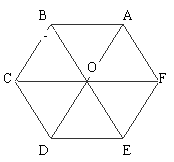 ② 不相等的向量一定不平行吗?
② 不相等的向量一定不平行吗?
③ 与零向量相等的向量必定是什么向量?
④ 与任何向量都平行的向量是什么向量?
⑤ 若两个向量在同一直线上,则这个向量一定是什么向量?
⑥ 两个非零向量相等的充要条件是什么?
⑦ 共线向量一定在同一条直线上吗?
(向量是仅由其大小与方向确定,特别要注重方向)
⑧ 指出右图出的平行向量、相等向量、共线向量、相反向量.
5.求两向量的和、差我们一般用三角形法则和平行四边形法则.
(注意,运用三角形法则时要注意两向量首尾相接,共线的两向量不适用)
二、教学例题:
例1.
已知单位向量![]() (方向分别为:东、南、西、北)求作向量
(方向分别为:东、南、西、北)求作向量![]() 、
、![]() . 变式:减变成加. (减法运算是加法运算的逆运算)
. 变式:减变成加. (减法运算是加法运算的逆运算)
例2.
计算:(1)![]() (2)
(2)![]()
(向量的数乘运算满足交换律、结合律、分配律)
三、巩固练习:
1.平行四边形ABCD中,![]() ,试用
,试用![]() 、
、![]() 表示向量
表示向量![]()
2.证明:![]() 并说明什么时候取等号?
并说明什么时候取等号?
(提示:用三角形法则画图证明)
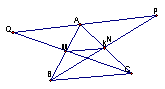 3.四边形
3.四边形![]() 的两条对角线相交于点M(1)若
的两条对角线相交于点M(1)若![]() ,
,
![]() (2)若
(2)若![]() 用
用![]() 、
、![]() 表示
表示![]()
4. 如图,知三角形ABC的两边AB、AC的中点分别为M、N,在BN的延长线上取点P,使得
NP=BN,在CM的延长线上取点Q,使MQ=CM. 试证明:P、A、Q共线.