高一数学同步单元测试（必修4）
任意角、弧度 任意角的三角函数 三角函数图像和性质
命题人 刘国钧中学 高级教师朱乔根
一、选择题：（5*12=60分）
1．函数
的定义域是 （ ）
A.
B. 
C. 
D. 
2．已知角α的终边过点P（4a,－3a）（a<0）,则2sinα＋cos α的值是 （ ）
A． B．－ C．0 D．与a的取值有关
3．若θ是第三象限角，且
，则
是 （ ）
A．第一象限角 B．第二象限角 C．第三象限角 D．第四象限角
4．已知A={第一象限角}，B={锐角}，C={小于90°的角}，那么A、B、C关系是（ ）
A．B=A∩C B．B∪C=C
C．A
C D．A=B=C
5．α为第二象限角，P(x, )为其终边上一点，且cosα＝x，则x值为( )
A． B．± C．－ D．－
6．的结果是( )
A．1 B．0 C．－1 D．
7．设sin123°＝a，则tan123°＝( )
A． B． C． D．
8．如果1弧度的圆心角所对的弦长为2，则这个圆心角所对的弧长为( )
A． B．sin0.5 C．2sin0.5 D．tan0.5
9．先将函数y＝sin2x的图象向右平移个单位，再将所得图象作关于y轴的对称变换，所得图象的解析式是( )
A．y＝sin(－2x＋)
B．y＝sin(－2x―)
C．y＝sin(－2x＋)
D．y＝sin(－2x―)
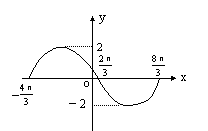
10．函数y＝Asin(ωx＋φ)在一个周期上的图象为上图所示．则函数的解析式是( )
A．y＝2sin(－) B．y＝2sin(＋)
C．y＝2sin(＋) D．y＝2sin(－)
11．下列函数中，周期为π，且在(0, )上单调递增的是( )
A．y＝tanx B．y＝cotx C．y＝sinx D．y＝cosx
12．若α满足＝2，则sinα·cosα的值等于( )
A． B．－ C．± D．以上都不对
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题：（16分）
13．已知sinθ－cosθ＝，则sin3θ－cos3θ＝＿＿＿＿＿．
14．函数y＝＋＋＋的值域为＿＿＿＿＿＿．
15．设θ∈（0，2π），点P（sinθ,cos2θ）在第三象限，则角θ的范围是 ．
16．函数y＝sin(－2x)的单调递增区间是＿＿＿＿＿＿＿＿＿＿
三、解答题：（74分）
17．已知扇形的周长为L，问当扇形的圆心角α和半径R各取何值时，扇形面积最大？（12分）
18．已知函数y＝3sin3x．
(1)作出函数在x∈[,]上的图象．
(2)求(1)中函数的图象与直线y＝3所围成的封闭图形的面积
(3)求f(x)的最小正周期；
(4)求f(x)的单调区间；
(5)求f(x)图象的对称轴，对称中心．（20分）
19．已知α为第三象限角，且f(α)＝．（14分）
(1)化简f(α)；
(2)若cos(α－)＝，求f(α)的值；
(3)若α＝－1860°，求f(α)的值．
20．（14分）已知函数f(x)=Asin
的图像与y轴交于点
。它与y轴右侧的第一个最大值点和最小值点分别为
。
(1) 求函数y=f(x)的解析式；
(2)用“五点法”作此函数在一个周期内的图像；
(3)说明它是由函数y=sinx的图像经过哪些变换而得到的．
21．（14分）是否存在α.β，α∈(－,)，β∈(0,π)，使等式sin(3π－α)＝cos(－β)，cos(－α)＝－cos(π＋β)同时成立？若存在，求出α,β的值，若不存在，请说明理由．
答案：
1．B 2．A3．B4．B5．C6．A7．D8．A 9．D10．D11．C
12．B提示：由条件得sinα＋8cosα＝0
tanα＝－8．
∴sinα·cosα＝＝＝＝－．
13．14．{－2,0,4}
17．解：∵L＝2R＋αR，S＝αR2．
∴α＝．
∴L＝2R＋2R2－LR＋2S＝0．
△＝L2－16S≥0S≤．
故当α＝2．R＝时，Smax＝．
18 略
19．(1)f(α)＝－cosα． (2) f(α)＝．
(3) f(α)＝－．
20．略
21．解：由条件得：
①2＋②2得：sin2α＋3cos2α＝2．
∴cos2α＝．
∵α∈(－,)．
∴α＝或－．
将α＝代入②得：cosβ＝，又β∈(0,π)．
∴β＝代入①适合，
将α＝－代入①得sinβ＜0不适合，
综上知存在满足题设．