高一数学期末综合练习
班级 姓名 学号 成绩
一、选择题:(每小题只有一个正确答案,将正确答案代号填入下表相应题号下)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
1. 在平行四边形ABCD中, ![]() +
+![]() +
+![]() 等于
等于
A.![]() B.
B.![]() C.
C.![]()
D.
D.![]()
2. 不等式![]() 的解集为
的解集为
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
3. 在![]() 中,
中,![]() ,则
,则![]() 等于
等于
A.![]() B.
B.![]() C.
C.![]() 或
或![]() D.
D.![]() 或
或![]()
4. 已知等差数列![]() 的公差为2,若
的公差为2,若![]() ,
,![]() ,
,![]() 成等比数列,则
成等比数列,则![]() 等于
等于
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5. 在![]() 中,若
中,若![]() 则
则![]() 的形状一定是
的形状一定是
A.等腰直角三角形 B.等腰三角形 C.直角三角形 D.等边三角形
6. ![]() 且
且![]() ,则
,则![]() 的最大值是
的最大值是
A.![]() B.
B.![]() C.
C.![]() D.不存在
D.不存在
7. 等比数列{an}的前3项的和等于首项的3倍,则该等比数列的公比为
A.-2 B.1 C.-2或1 D.2或-1
8. 函数![]() 的单调递减区间是
的单调递减区间是
A.![]()
![]() B.
B.![]()
![]()
C.![]()
![]() D.
D.![]()
![]()
9. 已知D点与A,B,C三点构成平行四边形,且![]() ,
,![]() ,
,![]() ,则D点坐标为
,则D点坐标为
A.(2,2) B.(4,6)
C.(-6,0) D.(2,2)或(-6,0)或(4,6)
10. 函数![]() 的部分图像是
的部分图像是
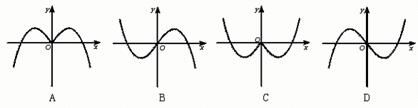
二、填空题:
11. 若![]() ,
,![]() ,
,![]() ,设
,设![]() ,
,![]() ,且
,且![]() ∥
∥![]() ,则
,则![]() 的值为
.
的值为
.
12. 已知![]() ,
,![]() ,则
,则![]() .
.
13. 在等差数列![]() 中,
中,![]() ,
,![]() ,则
,则![]() =
.
=
.
14. 等比数列的公比为2, 且前4项之和等于1, 那么前8项之和等于 .
15. 已知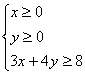 ,则
,则![]() 的最小值是
.
的最小值是
.
16. ![]() ,则和
,则和![]() 等于
.
等于
.
三、解答题:
17.
数列![]() 是首项为0的等差数列,数列
是首项为0的等差数列,数列![]() 是首项为1的等比数列,设
是首项为1的等比数列,设
![]() ,数列
,数列![]() 的前三项依次为1,1,2,
的前三项依次为1,1,2,
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)求数列![]() 的前
的前![]() 项的和.
项的和.
18.  运输公司有10辆载重量为6吨的A型卡车与载重量为8吨的B型卡车,有11名驾驶员.在建筑某段高速公路中,该公司承包了每天至少搬运480吨沥青的任务.已知每辆卡车每天往返的次数为A型卡车8次,B型卡车7次;每辆卡车每天的成本费A型车350元,B型车400元.问每天派出A型车与B型车各多少辆,公司所花的成本费最低,最低为多少?
运输公司有10辆载重量为6吨的A型卡车与载重量为8吨的B型卡车,有11名驾驶员.在建筑某段高速公路中,该公司承包了每天至少搬运480吨沥青的任务.已知每辆卡车每天往返的次数为A型卡车8次,B型卡车7次;每辆卡车每天的成本费A型车350元,B型车400元.问每天派出A型车与B型车各多少辆,公司所花的成本费最低,最低为多少?
19.
已知定点![]() ,动点
,动点![]() 在直线
在直线 ![]() 上,动点
上,动点![]() 在直线
在直线 ![]() 上,且
上,且![]() , 求
, 求![]() 面积的最小值.
面积的最小值.
20.
△![]() 中,内角
中,内角![]() 的对边分别为
的对边分别为![]() ,已知
,已知![]() 成等比数列,
成等比数列,![]() (Ⅰ)求
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)设![]() ,求
,求![]() 的值.
的值.
21. 5月份,有一新款服装投入某商场销售,5月1日该款服装仅销售出3件,5月2日售出6件,5月3日售出9件,5月4日售出12件,尔后,每天售出的件数分别递增3件,直到日销售量达到最大(只有一天)后,每天销售的件数开始下降,分别递减2件,到5月31日也刚好售出3件.
(Ⅰ)问5月几号该款服装销售件数最多?其最大值是多少?
(Ⅱ)按规律,当该商场销售此服装达到200件时,社会上就流行,而日销售量连续下降并低于20件时,则流行消失,问该款服装在社会上流行几天?说明理由.
高一数学期末综合练习
一、选择题:(每小题只有一个正确答案,将正确答案代号填入下表相应题号下)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | A | C | B | B | B | C | D | D | D |
11.3
12.![]() 13.24
13.24
14.17 15.1 16.1003
17.解:设等差数列的公差是![]() ,等比数列的公比是
,等比数列的公比是![]() ,则由
,则由![]()
![]() 得:
得:
![]()
![]() ,解得
,解得![]()
![]() ,
,
从而数列![]() 的通项公式是
的通项公式是![]() ,数列
,数列![]() 的通项公式
的通项公式![]()
数列![]() 的前
的前![]() 项的和是:
项的和是:
![]()
![]() .
.
18.解:设每天派出A型车与B型车各![]() 辆,并设公司每天的成本为
辆,并设公司每天的成本为![]() 元.由题意,得
元.由题意,得
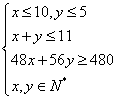 ,且
,且![]() .即
.即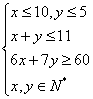
作出可行域,作直线![]() :
:![]() ,即
,即![]() .
.
作出一组平行直线:![]() 中(
中(![]() 为参数)经过可行域内的点和原点距离最近的直线,此直线经过
为参数)经过可行域内的点和原点距离最近的直线,此直线经过![]() 和
和![]() 的交点
的交点![]() ,由于点A的坐标不都是整数,而
,由于点A的坐标不都是整数,而![]()
![]() ,所以可行域内的点
,所以可行域内的点![]() 不是最优解.
不是最优解.
为求出最优解,必须进行定量分析.
因为,7×![]() +8×5≈69.2,所以经过可行域内的整点(横坐标和纵坐标都是整数的点)且与原点最小的直线是
+8×5≈69.2,所以经过可行域内的整点(横坐标和纵坐标都是整数的点)且与原点最小的直线是![]() ,在可行域内满足该方程的整数解只有
,在可行域内满足该方程的整数解只有![]() ,
,![]() ,
,
所以(10,0)是最优解,即当![]() 通过B点时,
通过B点时,
![]() 元为最小.
元为最小.
答:每天派出A型车10辆不派B型车,公司所化的成本费最低为3500元.
19.解:如图,设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
依题意有![]() ,
,![]()
而![]()
![]()
![]() .
.
20.解:(Ⅰ)由![]() ,得
,得![]()
由![]() 及正弦定理得
及正弦定理得 ![]()
于是![]()
![]()
![]()
![]()
(Ⅱ)由![]() ,得
,得![]() ,由
,由![]() ,可得
,可得![]() ,即
,即![]() .
.
由余弦定理 ![]() ,得
,得![]() ,
,
![]() .
.
21.解:本题的最终结果是:
| 日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 件数 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 日期 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 件数 | 33 | 36 | 39 | 37 | 35 | 33 | 31 | 29 | 27 | 25 |
| 日期 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 件数 | 23 | 21 | 19 | 17 | 15 | 13 | 11 | 9 | 7 | 5 |
| 日期 | 31 | |||||||||
| 件数 | 3 | |||||||||
(1)据此可知5月13日最多,是39件;
(2)5月12日(共有234件)开始流行,到5月22日,共11天。
22.证明:(1)∵ ![]() ,
,
∴ ![]() ,
,![]() ,
,![]() ,
,
三式相乘,则有![]() ;
;
(2)当![]() 时,
时,![]()
![]()
![]() ,
,
∴ ![]() ,不等式
,不等式![]() 仍成立。
仍成立。