高一数学试题
一、选择题(本大题共12小题,每小题5分,共60分)
1、 函数![]() 的递增区间是
的递增区间是
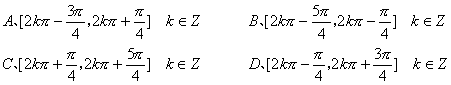
2、(理科)![]() 的取值范围是
的取值范围是
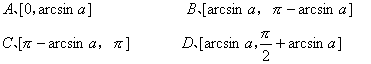
(文科)函数![]() 的最小正周期是
的最小正周期是
![]()
3、 数![]() 是奇函数,则
是奇函数,则![]() 等于
等于
![]()
4、(理科)若![]() 的值为
的值为
![]()
![]() (文科)已知
(文科)已知![]() 的值是
的值是
![]()
5、 函数![]() 的图象向左平移
的图象向左平移![]() 个单位,再将图象上各点的横坐标压缩为原来的
个单位,再将图象上各点的横坐标压缩为原来的![]() ,那么所得图象的函数表达式为
,那么所得图象的函数表达式为
![]()
6、 已知![]() 的值是
的值是
![]()
7、 函数![]() 的一个对称中心是
的一个对称中心是
![]()
8、(理科)若![]() 的值是
的值是
![]() B、
B、![]() C、0 D、-1
C、0 D、-1
(文科)已知![]() ,且
,且![]() 的终边在第二或第四象限,则sin
的终边在第二或第四象限,则sin![]() 等于
等于
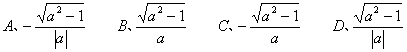
9、函数![]() 的图象的一条对称轴的方程是
的图象的一条对称轴的方程是
![]()
10、已知奇函数![]() 在[-1,0]上为单调递减函数,又
在[-1,0]上为单调递减函数,又![]() 为锐角三角形两内角,则
为锐角三角形两内角,则
![]()
11、函数![]() 是
是
A、周期是2π的奇函数 B、周期是π的偶函数
C、周期是π的奇函数 D、周期是2π的偶函数
12、若![]()
![]()
第Ⅱ卷(非选择题,共90分)
二、填空题(本大题共4小题,每小题4分,共16分)
13、求值:![]() = _______________。
= _______________。
14、![]() 是以5为周期的奇函数,
是以5为周期的奇函数,![]() =4,且
=4,且![]() =________。
=________。
15、给出下列命题:
= 1 * GB3 ①存在实数![]() =1成立;
=1成立;
= 2 * GB3 ②存在实数![]() 成立;
成立;
= 3 * GB3 ③函数![]() 是偶函数;
是偶函数;
= 4 * GB3 ④方程![]() 的图象的一条对称轴的方程。
的图象的一条对称轴的方程。
= 5 * GB3 ⑤若![]() 是第一象限角,且
是第一象限角,且![]() ,则
,则![]() 。
。
其中正确的命题的序号是___________________(注:把你认为正确的命题的序号都填上)。
16、已知![]() ,则函数
,则函数![]() 的值域是____________。
的值域是____________。
三、解答题(本大题共6小题,共74分。解答应写出文字说明、证明过程或演算步骤。)
17、(本小题满分10分)![]() 。
。
18、(本小题满分12分)
已知![]() ,求
,求![]() 的值。
的值。
19、(本小题满分12分)三角形ABC中,三个内角A、B、C的对边分别为![]() ,若
,若![]() ,求角C的大小。
,求角C的大小。
20、(本小题满分12分)已知2tanA=3tanB,求证:tan(A-B)=![]() 。
。
21、(本小题满分14分)设![]() 内有相异二实数解
内有相异二实数解![]() 。
。
1. 求常数![]() 的取值范围;
的取值范围;
2. 求![]() 的值。
的值。
22、(本小题满分14分)设![]() 为锐角,且
为锐角,且![]() 是否存在最大值与最小值?如果存在,请求出;如果不存在,请说明理由。
是否存在最大值与最小值?如果存在,请求出;如果不存在,请说明理由。
一、选择题答案:1、A 2、B 3、D 4、理科D,文科C 5、C 6、B
7、D 8、C 9、A 10、D 11、C 12、C
二、填空题答案:13、![]() 14、-4 15、 = 3 * GB3 ③、 = 4 * GB3 ④ 16、[-1,3]三、解答题17、
14、-4 15、 = 3 * GB3 ③、 = 4 * GB3 ④ 16、[-1,3]三、解答题17、![]()
18、由已知求出![]() ,进而可求
,进而可求![]() ,分母和差化积,即可得到原式=
,分母和差化积,即可得到原式=![]() 。
。
19、由![]() =cosB,故B=600,A+C=1200。
=cosB,故B=600,A+C=1200。
于是sinA=sin(1200-C)=![]() ,又由正弦定理有:
,又由正弦定理有:![]() ,从而可推出sinC=cosC,得C=450。
,从而可推出sinC=cosC,得C=450。
20、把tanA=![]() tanB代入tan(A-B)中,切化弦,即可证出。
tanB代入tan(A-B)中,切化弦,即可证出。
21、(Ⅰ)原方程化为![]() ,根据题意应有
,根据题意应有![]() 。
。
由已知有:![]()
移项,和差化积,即可得到![]() 。 22、可化得
。 22、可化得![]()
![]() 无最小值,有最大值1,从而原函数有最小值
无最小值,有最大值1,从而原函数有最小值![]() ,无最大值。
,无最大值。