高一数学习题
例1 已知![]() 、
、![]() ,则在以下各命题中,正确的命题共有( )
,则在以下各命题中,正确的命题共有( )
(1)![]() ,
,![]() 时,
时,![]() 与
与![]() 的方向一定相反
的方向一定相反
(2)![]() ,
,![]() 时,
时,![]() 与
与![]() 的方向一定相同
的方向一定相同
(3)![]() ,
,![]() 时,
时,![]() 与
与![]() 是共线向量
是共线向量
(4)![]() ,
,![]() 时,
时,![]() 与
与![]() 的方向一定相同
的方向一定相同
(5)![]() ,
,![]() 时,
时,![]() 与
与![]() 的方向一定相反
的方向一定相反
A.2个 B.3个 C.4个 D.5个
分析;要对以上5个命题进行真假判断,只要掌握关于实数![]() 与向量
与向量![]() 的积是一个向量,其方向规定为:当
的积是一个向量,其方向规定为:当![]() 时,
时,![]() 的方向与
的方向与![]() 的方向相同,当
的方向相同,当![]() 时,
时,![]() 的方向与
的方向与![]() 的方向相反,就不难作出正确选择.
的方向相反,就不难作出正确选择.
解:根据实数![]() 与向量
与向量![]() 的积
的积![]() 的方向的规定,易知命题(1)、(2)、(3)都是正确的.
的方向的规定,易知命题(1)、(2)、(3)都是正确的.
对于命题(4)与(5),(ⅰ)![]() ,可得
,可得![]() 、
、![]() 同为正或同为负,所以
同为正或同为负,所以![]() 与
与![]() 或者都与
或者都与![]() 同向,或者都与
同向,或者都与![]() 反向,所以
反向,所以![]() 与
与![]() 同向.故命题(4)是正确的;(ⅱ)若
同向.故命题(4)是正确的;(ⅱ)若![]() ,则
,则![]() 与
与![]() 异号,与
异号,与![]() 与
与![]() 中,一个与
中,一个与![]() 同向,一个与
同向,一个与![]() 反向,∴
反向,∴![]() 与
与![]() 反向,故命题(5)也是正确的.
反向,故命题(5)也是正确的.
综上所述,应选择(D).
例2计算:
(1) ![]() ;
;
(2)![]()
解:(1)原式![]()
(2)原式
![]()
评注:实数与向量的积的运算法则类似于整式的加减运算法则。
例3 如图(1),已知向量![]() 、
、![]() ,求作向量
,求作向量![]()
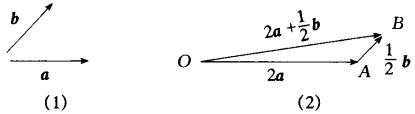
解:在平面上任取点O,作![]()
![]() ,
,![]()
![]() ,则
,则![]()
![]() ,如图(2)。
,如图(2)。
评注:作向量![]()
![]() ,要使
,要使![]() 与
与![]() 同向,且
同向,且![]() 的长度等于
的长度等于![]() 的长度的2倍;作
的长度的2倍;作![]()
![]() 则同理可作。
则同理可作。
例4 如图,D是△ABC中BC边的中点,
求证:![]()
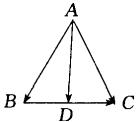
证法一:∵D是BC边的中点,
![]()
![]()
证法二:延长AD到E,使DE=AD,连BE、CE,如图,则四边形ABCE是平行
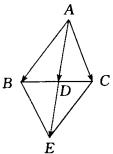 四边形.
四边形.
由向量加法的平行四边形法则知:
![]()
![]()
![]()
例5 已知![]() 、
、![]() 不共线,
不共线,![]() ,
,![]() ,试判断
,试判断![]() 与
与![]() 是否共线?
是否共线?
分析;要判断![]() 与
与![]() 是否共线,只要看是否存在实数
是否共线,只要看是否存在实数![]() ,使
,使![]()
解:∵![]() ,
,
![]() ,
,
∴![]()
∴![]() 与
与![]() 共线。
共线。
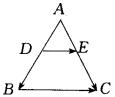 例6 已知三角形ABC,
例6 已知三角形ABC,![]() ,
,![]() ,点D、E分别在线段AB和AC上,且
,点D、E分别在线段AB和AC上,且![]() ,证明
,证明![]()
证明:如图,设![]() (
(![]() ,
,![]() ),则
),则
![]() ,
,
![]()
![]()
![]()
例7 设平面上有点P和△ABC,已知![]()
![]() ,试确定P的位置。
,试确定P的位置。
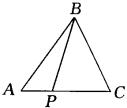 解:∵
解:∵![]() ,则由题意得:
,则由题意得:
![]() ,
,
即![]() ,
,
∴ 点P在线段AC上,且将线段AC分成![]() (如图)
(如图)
例8 已知:△ABC和点G,
试证:点G是△ABC的重心的充要条件是:![]()
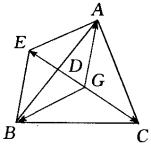 证明:如图,以线段GA和GB为邻边作
证明:如图,以线段GA和GB为邻边作![]() ,连EG交AB于D,则D是AB 的中点,且
,连EG交AB于D,则D是AB 的中点,且![]()
![]() ,
,![]() ,
,
![]()
充分性:若![]() ,则
,则![]() ,
,
![]()
∴G是△ABC的重心。
必要性:若G是△ABC的重心,则因D是AB边的中点,所以有![]() ,
,
∴![]()
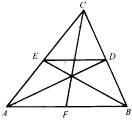 例9 如图,已知△ABC中,D、E、F分别是BC、CA、AB的中点,
例9 如图,已知△ABC中,D、E、F分别是BC、CA、AB的中点,
求证:(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
点拨:要证明(1)只须证明![]()
![]() ;要证(2)只须证明
;要证(2)只须证明![]()
![]()
![]() 对于(3),可将等式左边诸向量代换成一些有明显关系的向量再进行运算。
对于(3),可将等式左边诸向量代换成一些有明显关系的向量再进行运算。
证明:
![]()
![]()
这说明![]()
∴
![]()
![]()
∴![]()
![]()
![]()
∴ ![]()
![]()
同理,![]() ,
,
![]() ,
,
∴ ![]()
![]()
![]()
点评:用向量方法来证明平面几何命题,应先把结论写成向量形式,然后通过向量运算来完成,而不是通过平面几何的公理体系来完成.
例10 在△ABC中(右图),设D及E是BC的三等分点,D在B和E之间,F是AC的中点,G是AB的中点,又设H是线段EG和DF的交点,试用向量法求比值![]()
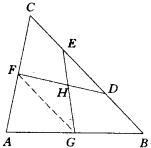 解:设
解:设![]() ,
,![]() ,则
,则![]()
![]() ,现在把上式中的每一个向量用
,现在把上式中的每一个向量用![]() 及
及![]() 表示:
表示:
![]() ,
,
![]()
![]()
![]()
![]() ,
,
![]() ,
,
![]()
![]()
![]()
![]()
把这些式子代入前面的等式,我们有
![]()
![]()
即![]()
![]()
由于![]() ,
,![]() 不共线,所以
不共线,所以
解之![]()
从而得![]()
说明:上述求解过程中没有利用平面几何中的有关结论。其实采用纯平几法求解是十分简洁的。
例11 已知向量![]() ,
,![]() ,其中
,其中![]() 、
、![]() 不共线,向量
不共线,向量![]() ,问是否存在这样的实数
,问是否存在这样的实数![]() 、
、![]() ,使向量
,使向量![]() 与
与![]() 共线?
共线?
解:∵ ![]()
![]()
要![]() 与
与![]() 共线,则应有实数
共线,则应有实数![]() ,使
,使![]() ,
,
即![]() ,
,
由![]() 得
得![]()
故存在这样的实数![]() 、
、![]() ,只要
,只要![]() ,就能使
,就能使![]() 与
与![]() 共线。
共线。
评注:向量![]() 与
与![]() 共线,则必有
共线,则必有![]() 请问:若
请问:若![]() ,向量
,向量![]() 与
与![]() 共线吗?
共线吗?
例12 如图,![]() 、
、![]() 不共线,点P是直线AB上的一点,且
不共线,点P是直线AB上的一点,且![]() (
(![]() ,
,![]() ),试用
),试用![]() 、
、![]() 表示
表示![]() 。
。
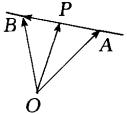 分析:
分析:![]() 与
与![]() 、
、![]() 没有直接的联系,这时我们可以在△OAP(或△OPB)中,把
没有直接的联系,这时我们可以在△OAP(或△OPB)中,把![]() 用
用![]() 和
和![]() (或
(或![]() 与
与![]() )表示出来。
)表示出来。
解:![]()
![]()
![]()
![]()
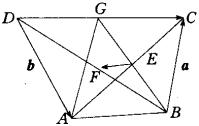 例13 如图,点E、F分别为四边形ABCD的对角线AC,BD的中点,设
例13 如图,点E、F分别为四边形ABCD的对角线AC,BD的中点,设![]() ,
,![]() ,试用
,试用![]() 、
、![]() 表示
表示![]() 。
。
错解:连BE并延长交CD于G,连AG。由于E是AC与BG的中点,所以四边形ABCG是平行四边形。因此![]() 、
、![]()
![]()
又∵F是BD的中点,
![]()
![]()
点击:由于四边形ABCD不是梯形,而是一般的四边形.所以,点E是AC的中点,但并不一定是BG的中点.因此,四边形ABCG并不一定是平行四边形,所以![]() 不一定等于
不一定等于![]() ,故上述解法是错误的.
,故上述解法是错误的.
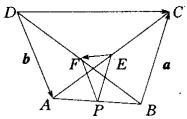 正解:如图,取AB中点P,连EP、FP。
正解:如图,取AB中点P,连EP、FP。
在△ABC中,EP是与BC平行的中位线,
![]()
在△ABD中,FP是与AD平行的中位线,
![]()
在△EFP中,![]()
![]()
![]()
说明:由于![]() ∴
∴![]() ,
,
![]() 。即
。即![]() 也等于四边形另一对对边相应向量和的一半。
也等于四边形另一对对边相应向量和的一半。