高一数学第二学期期末考试数学试卷
一、选择题：本大题共12小题，每小题5分，共60分.
1、设
，那么下列的点在角
的终边上的是（ ）
（A） （4，－3） （B） (－4,3) (C) (3,－4) (D) (－3,4)
2、若
，则不等式
的解集为（ ）
（A）
（B）
（C）
（D）
3、已知函数
，若
，则
（ ）
（A） 
（B） 2 （C）
（D） －2
4、把函数
的图像按向量
平移后得到的图象的解析式为（ ）
（A）
（B）
（C）
（D）
5、等差数列
的通项公式为
，那么的前
项和为（ ）
（A） 
（B） 
（C） 
（D）
6、已知D、E、F分别是△ABC三边，AB、BC、CA的中点，则
的值为（ ）
（A） 2 （B） 1 （C） (D) 
7、已知
，
，则
等于（ ）
（A） 
（B） 
（C） 
(D) 
8、下列函数中以
为周期，图象关于直线
对称的函数是（ ）
（A）
（B）
（C）
（D）
9、若A（3，－6）、B（－5，2）、C（6，－9）则A分
的比
为（ ）
（A） 
（B） 
（C）
（D）
10、若
，
，
，则
值为（ ）
（A） 
（B） （C） 
（D） 0
11、已知
中，角
的对应的边分别为
，
，若该三角形的边
有两个不同的值，则的取值范围是（ ）
（A） 
（B） 
（C） 
(D) 
12、设向量
不共线，则关于的方程 
的解的情况是（ ）
（A）至多只有一个实数解 （B）至少有一个实数解 （C）至多有两个实数解 （D）可能有无数个实数解
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
|
|
二、填空题：本大题共4小题，每小题4分，共16分.
13、若将向量
绕原点按逆时针方向旋转
得到向量
，则向量的坐标为__________.
14、已知
均为锐角，
，则
.
15、函数
的单调递减区间为_________________________.
16、下面给出的四个命题：
①若
，则
②若
，则
③若的夹角为
，那么
④对一切向量，都有
成立，正确的命题的序号为_______（将所有正确命题都填上）.
三、解答题（本大题共6小题，共74分，解签应写出文字过程，证明过程或演算步骤）
17、（12分）中，已知
，面积
，求的三边长.
18、（12分）已知向量
，求
的值.
19、（12分）已知函数
，其中
。
(1)当
时，求函数
的最大值与最小值.
(2)求的取值范围，使
在区间
上为单调函数.
20、（12分）设
是直角坐标系中，x轴、y轴正方向上的单位向量，设
(1)若(
,求
.
(2)若
时，求的夹角的余弦值.
(3)是否存在实数，使
，若存在求出的值，不存在说明理由.
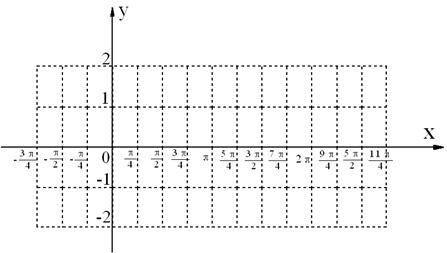
21、（12分）已知
.
(1)设
，试在如图所给的直角坐标系中，画出函数在
上的简图.
(2)设方程
在
上的三个正根依次成等比数列，求实数
的值.
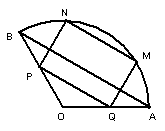
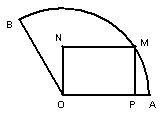
22、（14分）将一块圆心角为
，半径为
的扇形铁片裁成一块矩形如图所示有两种裁法，（1）让矩形一边在扇形的一条半径
上；(2)让矩形的一边与弦
平行.
请问，哪种裁法能得到最大面积的矩形？并求出这个最大值.
