高一数学第二学期月考检测
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分。
班级 姓名 学号 得分 2006.3.8
第Ⅰ卷 (选择题 共60分)
一、选择题：（本大题共计12小题，每小题5分，共60 分）
1、若
是第一象限角，则
是（ ）
A、第一象限 B、第一、四象限角 C、第二象限角 D、第二、四象限角
2、若角
的终边关于y轴对称，则的关系一定是（k∈Z）（ ）
A、
B、
C、
D、
3、设角的终边有一点P（2sin30°，--2cos30°）则sin的值 （ ）
A、
B、
C、
D、
4、下列各三角函数值：
其中负值的个数是（ ）
A、1个 B、2个 C、3个 D、4个
5、已知
且
共线。则
的关系是（ ）
A、共线 B、不共线 C、可共线，可不共线 D、不能确定
6、已知
，且
则
的值 （ ）
A、
B、
C、
D、
7、如果f(sinx)=cos2x，那么f(cosx)等于（ ）
A、 
B、
C、
D、
8、函数
的周期是（ ）
A、2π B、π C、
D、
9、函数
的定义域，值域分别是（ ）
A、R，[0，1] B、R+，[--1，1] C、R，[--1，1] D、R+，[0，1]
10、函数y=sin(-2x)的单调递减区间是（ ）
A、
B、
C、
D、
11、要得到y=tan2x的图象，只需把
的图象（ ）
A、向左平移
个单位 B、向右平移个单位
C、向左平移
个单位 D、向右平移个单位
12、已知函数
的图象上相邻的一个最大值与一个最小值点恰好在圆x2+y2=R2上则f(x)的最小正周期是 （ ）
A、1 B、2 C、3 D、4
一. 选择题（每小题5分，共60分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
|
|
第二卷（非选择题共90分）
二. 填空题：（本大题共6小题，每小题4分，共24分，请把答案直接填在题中横线上）
13、钟表经过10分钟，时针转了 度，若将钟表拔慢了10分钟，分针转了 度。
14、若点P（3a-9，a+2）在角的终边上，且
则实数a的取值范围是
。
15、若函数
的最小正周期为T且T∈（1，3）则正整数
的最大值是
。
16、给出下列命题
①函数y=sinx不是周期函数
②函数y=cosx的周期为π
③
是偶函数
④
的一个对称中心是
⑤
的一条对称轴
其中正确的命题的序号是
三．解答题(本大题5小题, 共74分, 解答应写出文字说明、证明过程或演算步骤)
17、已知
（15分）
求
（2）
（3）
18、设有函数
和函数
(a>0,b>0,k>0)，若它们的最小正周期之和为
，且
。求这两个函数的解析式。（14分）
19、已知函数
的图象的一个最高点为
，由这个最高点到相邻最低点，图象与x轴交于（6，0）点。
（1）求这个函数的解析式；
（2）用“五点法”画出该函数图象的简图；
（3）由函数y的图象是否可以经过平移变换得到一个奇函数的图象？说明理由。（16分）
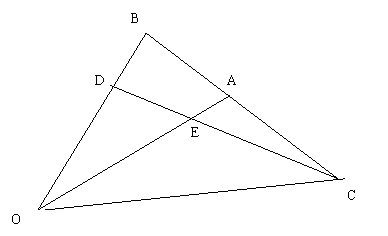
20、已知三角形
中，点C是点A的对称点，点D是线段OB的一个高近B的三分点，DC和OA交于E，设
（1）
求向量
（2）如
，求实数
的值。 (13分)
21、已知某海滨浴场海浪的高度y米是时间t（
，单位小时）的函数记作y=f(t)，下表是某日各时的浪高数据：
| t(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y（米） | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1 | 0.5 | 0.99 | 1.5 |
经过长期观测y=f(t)的曲线可近似地看成是函数y=Acost+b
（1）根据以上数据求函数y的最小正周期T，振幅A及解析式
（2）依据规定，当海浪高度高于1米时才对冲浪爱好者开放，请依据（1）的结论，判断一天内的上午8：00时至晚上20：00时之间，有多少时间可供冲浪者进行运动？（16分）