高一数学第一次月考
班级___________ 姓名___________ 座号________ 总分_______
一、选择题（本题共10题，每题5，共50分，并把正确答案填在下表中）
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|
|
|
|
|
|
|
|
|
|
|
1．下列四个关系式中，正确的是（ ）。
（A）
(B) 
(C ) 
(D) 
2．全集
，集合
，
则
（ ）。
（A）
(B) 
(C
) 
(D) 
3． 集合
，
，
,
,则下面包含关系中不正确的是（ ）。
（A）
(B) 
(C) 
(D) 
4．已知集合M=｛x ∈N 8－x∈N｝，则M中元素的个数是（ ）。
（A） 10 (B) 9 (C ) 8 (D) 无数个
5．集合｛2，4，6，8｝的真子集的个数是（ ）。
（A）16 (B)15 (C)14 (D) 13
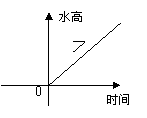
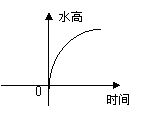
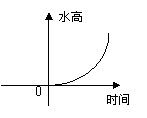
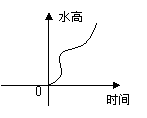
6．给右图的容器甲注水，下面图像中哪一个图像可以大致刻画容器中水的高度与时间的函数关系：（ ）。
 |  | ||||
 | |||||
(A) (B)
 |  |
容器甲
(C) (D)
7．下列各组函数中，表示同一函数的是（ ）。
A．
B．
C ．
D．
8．已知
是偶函数，且
，那么
的值为（ ）。
（A） 5 (B) 10
(C ) 8 (D) 不确定
9．集合
，
，给出下列四个图形，其中能表示以M为定义域，N为值域的函数关系的是（
）。
 |
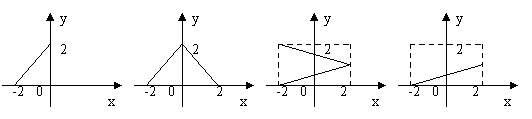（A） (B) (C ) (D)
10．如果函数
=x
+2(a-1)x+2在区间(－∞，4)上是减函数，则实数a的取值范围是（ ）。
A．a≥－3 B. a≤－3 C. a≤5 D. a≥3
二、填空题（本题共4题，每题5，共20分）
11. 集合M={a
∈N，且a∈Z}，用列举法表示集合M=_
12.
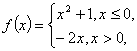若
，则 x= .
13. 函数
的定义域是________________
14. 若=－x+2ax与g
=
在区间 [1，2]上是减函数，则a的取值范围是__________
三、 解答题:(解题必须有详细的解题过程)
15. 已知集合A=｛x x+x－6=0｝，B=｛x mx+1=0｝，若B
A，求由实数m所构成的集合M。(本小题12分)
16.已知R为全集，A=｛x －1≤x＜3｝， B=｛x 
≥1｝，求(
UA)
B
（本小题13分）。
17. 判断并证明函数= x
+
在(0,＋∞)上的奇偶性（本小题13分）。
18. 若函数
的定义域为（－
，2），求
的定义域（本小题14分）。
19. A、B两城相距100km，在两地之间距A城xkm处D地建一核电站给A、B两城供电，为保证城市安全，核电站距市距离不得少于10km。已知供电费用与供电距离的平方和供电量之积成正比，比例系数
。若A城供电量为20亿度/月，B城为10亿度/月。（本小题14分）
（Ⅰ）把月供电总费用y表示成x的函数，并求定义域；
（Ⅱ）核电站建在距A城多远，才能使供电费用最小。
20. 已知函数f ( x )=x 2+ax+b，且对任意的实数x都有f (1+x)=f (1－x) 成立。
（本小题14分）
（Ⅰ）求实数 a的值；
（Ⅱ）利用单调性的定义证明函数f(x)在区间[1，＋∞
上是增函数。