高一数学第一学期第二次阶段性测试试卷

高一数学第一学期第二次阶段性测试试卷

命题人：李春瑜　　　审题：张春林

第Ⅰ卷

一．选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中只有一项符合题目要求）

1.定义A-B=若M={1,2,3,4,5},N={2,3,6},则M-N=　　　　　  (　　　 )

A.M　　　 B.N　　　  C.{1,4,5}　　　　D.{6}

2.设集合A,B都是实数集,映射f:AB把集合A中的元素x映射到集合B中的元素x³-x+1,则在f下,象1的原象组成的集合是　　　　　　　　　　　　　　　　　　　  (　　　 )

A.{1}　　　　　 B. {0,1,-1}　　　　　 C.{0}　　　　 D. {0,-1,-2}

3.设　　　　　　　　  ,则a,b,c的大小关系是　　　　　　　　　　　　　　  (　　　)

A.a>b>c　　　 B.b>a>c　　　　  C.c>a>b　　　　　  D.a>c>b

4.函数的零点位于的区间是　　　　　　　　　　　　　　　　 (　　 )

A.(0,1)　　　 B.(1,2)　　　　　　 C.(2,3)　　　　　 D.(3,4)

5.设,则关于x的方程　　　　　　　　　  (　　 )

A.必有唯一解　　　B.必无解　　　 C.当a>1时有唯一解　 D. 当0<a<1时有唯一解

6.在空间四边形ABCD的AB，BC，CD，DA上分别取点E,F,G.H,如果EF与HG相交于一点M,那么M　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  (　　)

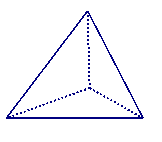A.一定在直线AC上　　　　　 B. 一定在直线BD上

C.在直线AC,BD上都有可能　　D.不在这两条直线上　　　　　　　　　  A

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D

　　　　　　　　　　　　　　　　　　　　　　　　　　 B　　　　　　　　  C

7.一个水平放置的平面图形的斜二测直观图是一个底角为,腰和上底均为1的等腰梯形,则这个平面图形的面积是　  　　　　　　　　　　　　　　　　　　　　　　(　　 )

A.　　　　　　　  B.1+　　　　  C.1+　　　 D. 2+　

8.设A,B,C表示不同的点,表示不同的直线,α,β表示不同的平面,下列推理不正确的是　  (　　 )

A.　　  B　　　　　

C.　　　　　　  D.

9. 已知lg2=a,lg3=b,则等于　　　　　　　　　　　　　　　　　　　　 (　　　 )

A.　　　　　　　　  B. 　　　　　　 C. 　　　　　 D.

10.某种商品提价25％,现在要恢复原价,则应降价　　　　　　　　　　　　　　 (　　 )

A. 25％　　　　  B. 15％　　　　 C. 10％　　　　　 D. 20％

11.已知函数,则　　　　　　　　　　　　  (　　　)

A.ab>1　　　　  B.ab<1　　　　  C.ab=1　　　　　  D.(a-1)(b-1)>0

12.奇函数f(x)在(0,+∞)上是增函数,且f(-3)=0,则xf(x)<0的解是　　　　　　  (　　　)

A.(-3,0)∪(3, +∞)　　　　　　　　 B.(- ∞,-3)∪(0,3, )　　

C. (- ∞,-3)∪(3, +∞)　　　　　　  D. (-3,0)∪(0,3, )　

第Ⅱ卷

二．填空题（本大题共4小题，每小题4分，共16分，将正确答案写在题中的横线上）

13．已知函数　　　　　　　　　　　　　　  ____________________;

14.函数的单调增区间是_____________________;

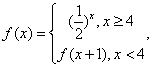15.已知函数　　　　　　　　　　　　 则=________________;

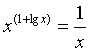16.方程　　　　　  的解是_____________________.

三.解答题(本大题共6小题，共74分.解答应写出文字说明,证明过程及演算步骤)

17(本小题12分)

计算(1)　　　　　　　　　　　　  ；

　(2) 已知10^m=4,10ⁿ=9,求　　　 ；

　(3) .

18. (本小题12分)

已知直线AB//直线CD,直线MN∩AB=M,直线MN∩CD=N,求证:直线AB,CD,MN共面.

19. (本小题12分)

已知二次函数f(x)=ax²+bx+c满足条件f(2+x)= f(2-x),其图象的顶点为A，以图象与x轴交于B，C两点，其中B点坐标为（-1，0），△ABC的面积s=54,试确定这个二次函数的解析式.

20. (本小题12分)

已知集合A={yy²-(a²+a+1)y+a(a²+1)>0},B={yy=　　　　　　　　  },若,求实数a的取值范围.

21. (本小题12分)

某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,全部租出,当每辆车的月租金每增加50元时,未租出的车将会增加一辆,租出的每辆车公司每月需支付维护费200元.

(1)　 当每辆车的月租金为3600元时,能租出多少辆车?

(2)　 当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大收益是多少?

22．(本小题14分)

设函数f(x)=ax²+bx+1　 (a,b为实数，且a>0)

　　（1）若f(－1)=0，且对任意实数均有f(x)≥0成立，求f(x)的表达式；

（2）在（1）的条件下，当x∈[－2，2]时，g(x)=f(x)－kx是单调函数，求实数k的取值范围。

（3）若f(x)是偶函数，试判断F(x)的奇偶性；

（4）设mn<0，m+n>0，且f(x)是偶函数，求证：F(m)+F(n)>0