高一数学第一学期第一次检测
试 卷 .
(考试时间:120分钟,分值150分)
一、选择题(本题共11小题,每小题5分,计55分;每小题只有一个正确答案,请将正确答案的字母序号填入下页的答题纸上。)
1、设全集u={0,1,2,3,4},集合A={0,1,2,3},集合B={2,3,4},则(CuA)∪(CuB)=
(A)、{0}; (B)、{0,1}; (C)、{0,1,4}; (D)、{0,1,2,3,4}。
2.已知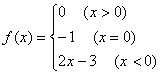 ,则
,则![]() 的值是
的值是
(A)、0; (B)-1; (C)5; (D)-5。
3.若函数![]() =
=![]() 在
在![]() 上是减函数,则
上是减函数,则
(A)![]() ; (B)
; (B)![]() ; (C)
; (C)![]() ; (D)
; (D)![]() 。
。
4.设f:A→B是从集合A到B的映射,如果A中的元素a在法则f下与B中的元素b对应,那么a叫做b的原象,b叫做a的象。下列命题正确的是
(A) B中的每一个元素在A中的原象是唯一的;
(B) A中的不同元素在B中的象必不相同;
(C) B中的每一个元素在A中必有原象;
(D) A中的每一个元素在B中必有唯一的象。
5.下列各组中的两个函数表示同一函数的是
(A) f (x)=x0与g (x)=1
(B) f (x)=x与g (x)=![]()
(C) f (x)=x与g (x)=![]() (D) f (x)=
(D) f (x)=![]() 与g (x)=
与g (x)= ![]()
6.![]() ,其中a,b,c,d是常数,
,其中a,b,c,d是常数,![]() ,则f(7)=
,则f(7)=
(A)7 (B)14 (C)17 (D)21
7.函数y=![]() 的定义域为
的定义域为![]() ,则函数
,则函数![]() 的定义域是
的定义域是
(A)![]() ; (B)
; (B)![]() ; (C)
; (C)![]() ; (D)
; (D)![]() 。
。
8.
若![]() 为偶函数,则
为偶函数,则![]() 在区间
在区间![]() 上是
上是
(A)增函数 (B)减函数
(C)部分是增函数,部分是减函数 (D)以上都不对。
9、已知y=f(x)的值域为[0,1]则y=f(x-1)的值域为
(A)[1,2] (B)[-1,0] (C)[-1,2] (D)[0,1]
10、已知函数![]() 在
在![]() 上是增函数,函数
上是增函数,函数![]() 是偶函数,则
是偶函数,则
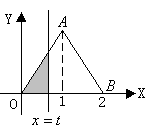 (A)
(A)![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
11、如右图,在直角坐标系的第一象限内,![]() 是边长
是边长
为2的等边三角形,设直线![]() :
:![]()
![]() 截这
截这
个三角形所得直线位于直线左侧的图形的面积为![]() ,
,
 |
则函数
(A) (B) (C) (D)
二、填空题(每小题4分,共5小题计20分;请将答案填在下页的答题纸上)
12、满足{a,b}![]() {a,b,c,d,e}的集合A有
个。
{a,b,c,d,e}的集合A有
个。
13、f :A→B是从A到B的映射,其中集合A = B = {( x,y ) x,y∈R },
![]() .那么B中元素(-5,2)的原象是
。
.那么B中元素(-5,2)的原象是
。
14、已知函数f(x)=![]() ,那么f(x)是
,那么f(x)是
(用奇函数、偶函数、既奇且偶函数、非奇非偶函数填空)
15、 函数y =![]() 的递减区间是
的递减区间是
16、函数y=f(x)的定义域为![]() ,若
,若![]() 的定义域是
的定义域是
| 题次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 答案 |
 高一数学第一次检测答题纸
高一数学第一次检测答题纸
成绩____________
一、选择题
二、填空题
12、__________________________ 13、__________________________
14、__________________________ 15、__________________________
16、__________________________
三、解答题(共6题,满分75分)
17、(本题10分).已知集合A={xx2+3x+2 >0},B={xx2-7x+12≥0},
C={x2-x<0},求(A∩B)∩C
18、(本题12分)知函数![]() 是R上的偶函数,当
是R上的偶函数,当![]() ≥0时,
≥0时,![]() 。
。
(1)用分段函数写出函数![]() 表达式;
表达式;
(2)指出其单调区间;
(3)指出在什么区间上![]() >0,在什么区间上
>0,在什么区间上![]() <0;
<0;
(4)求函数的最值.
19、(本题12分)求证:函数![]() 在区间
在区间![]() 上是单调增函数。
上是单调增函数。
 20、(本题13分)若非空集合
20、(本题13分)若非空集合![]() ,
,![]() ,
,![]() ,求实数
,求实数![]() 的集合。
的集合。
21、(本题14分)已知函数![]() 在区间[0,3]上有最小值-2,求实数m的值。
在区间[0,3]上有最小值-2,求实数m的值。
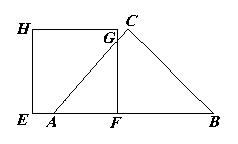
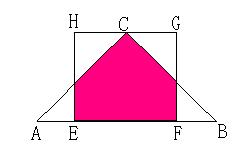 22、(本题14分)如图△ABC为等腰直角三角形,斜边AB长为2,边长为1的正方形EFGH的边EF与AB在同一直线上,若先使F与A重合,然后使正方形向右运动,直到E与B重合为止,设F离A的距离为x,正方形与三角形的公共部分的面积为 f(x), 试写出函数f(x)的解析式,并求出函数的值域。
22、(本题14分)如图△ABC为等腰直角三角形,斜边AB长为2,边长为1的正方形EFGH的边EF与AB在同一直线上,若先使F与A重合,然后使正方形向右运动,直到E与B重合为止,设F离A的距离为x,正方形与三角形的公共部分的面积为 f(x), 试写出函数f(x)的解析式,并求出函数的值域。