高一数学第一学期期末调研考试试题
本试卷卷面总分100分,考试时间100分钟,考试形式闭卷
| 题号 | 一 | 二 | 三 | 总分 | |||
| 16 | 17 | 18 | 19 | ||||
| 得分 | |||||||
一、选择题(每题4分,计40分.)
1.设![]() 是第四象限角,则下列不等式成立的是
是第四象限角,则下列不等式成立的是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.下列判断,正确的是
A.若两个向量相等,则它们的起点和终点分别重合
B.模相等的两个平行向量是相等的向量
C.若![]() 和
和![]() 都是单位向量,则
都是单位向量,则![]() =
=![]()
D.如果![]() 、
、![]() 是同一平面内两个不共线的向量,那么对于这一平面内的任一向量
是同一平面内两个不共线的向量,那么对于这一平面内的任一向量![]() ,有且只有一对实数m、n使得
,有且只有一对实数m、n使得![]() =m
=m![]() +n
+n![]()
3.已知集合M=![]() 、集合N=
、集合N=![]() .则集合M与N之间的关系是
.则集合M与N之间的关系是
A. M=N B. M![]() N C. N
N C. N![]() M D.M
M D.M![]() N=
N=![]()
4.要得到函数![]() 的图象,只需将函数
的图象,只需将函数![]()
A.向左平移![]() 个单位
B.向左平移
个单位
B.向左平移![]() 个单位
个单位
C.向右平移![]() 个单位
D.向右平移
个单位
D.向右平移![]() 个单位
个单位
5.某种储蓄按复利计算利息,若本金为1元,每期利率为![]() ,设存期是
,设存期是![]() ,本利和(本金加上利息)为
,本利和(本金加上利息)为![]() 元.则本利和
元.则本利和![]() 随存期
随存期![]() 变化的函数关系式为
变化的函数关系式为
A.![]() B.
B.![]()
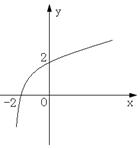 C.
C.![]() D.
D.![]()
6. 已知函数![]() 的图象如右图所示,则
的图象如右图所示,则![]() 的值分别为
的值分别为
A.![]() ,3 B.
,3 B.![]() ,-3
,-3
C. 3,3 D. 3,-3
7.已知定义域为R的偶函数![]() 在
在![]() 上是增函数,若
上是增函数,若![]() ,则
,则![]() 、
、![]() 的大小关系是
的大小关系是
A.![]()
![]()
![]() B.
B.![]()
![]()
![]()
C.![]() =
=![]() D.无法确定
D.无法确定
8.设![]() ,
,![]() ,
,![]() ,则
,则![]()
A.![]() B.
B.![]()
C.![]() D.
D.![]()
9.函数![]() 的值域是
的值域是
A.
![]() B.
B.
![]() C.
C.
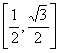 D.
D.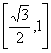
10.下列各式计算结果不可能为![]() 的是
的是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
二、填充题(每题4分,计20分)
11.已知函数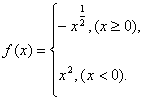 则
则![]() .
.
12.已知角![]() 的终边经过点
的终边经过点![]()
![]() .则
.则![]() .
.
13.设![]() ,
,![]() ,
,![]() .则
.则![]() 、
、![]() 、
、![]() 的大小关系为_____ .
的大小关系为_____ .
14.已知函数![]() 是奇函数,则
是奇函数,则![]() .
.
15.在Rt![]() 中,
中,![]() ,设
,设![]() ,
, ![]() ,则
,则![]() =
.
=
.
三、解答题(共4题,计40分)
16.(本题9分)
已知:![]() ,
, ![]() ,
,
![]() ,
,![]() .求证:
.求证:![]() .
.
17.(本题12分)
已知函数![]() ,
,![]() 为常数
为常数
(1)求![]() 在
在![]() 上的最大值;
上的最大值;
(2)若![]() 在
在![]() 有且仅有一个根,求
有且仅有一个根,求![]() 的范围;
的范围;
(3)当![]() =2时,利用计算器,用二分法求在[2,3]内的近似解(精确到0.1),并写出方程
=2时,利用计算器,用二分法求在[2,3]内的近似解(精确到0.1),并写出方程![]() 精确解
精确解![]() 这时所在的区间.
这时所在的区间.
1
18.(本题8分)
一半径为3 m的水轮如图所示,水轮圆心O距离水面![]() m,已知水轮每分钟逆时针地转动4圈,如果当水轮上点P从水中浮现时(图中点P0)开始计算时间.试根据图中建立的直角坐标系,解答下列问题:
m,已知水轮每分钟逆时针地转动4圈,如果当水轮上点P从水中浮现时(图中点P0)开始计算时间.试根据图中建立的直角坐标系,解答下列问题:
(1)将点P距离水面的高度![]() (m)表示为时间
(m)表示为时间![]() (s)的函数;
(s)的函数;
(2)点P第一次到达最高点需要多长时间?
19.(本题11分)
已知函数![]() (
(![]() 为非零常数)在
为非零常数)在![]() 上恒有意义.
上恒有意义.
(1)确定![]() 的取值范围;
的取值范围;
(2)证明![]() 上为单调增函数;
上为单调增函数;
(3)求![]()
![]() 上的最小值.
上的最小值.
高一数学试题参考答案及格评分标准
选择题
CDBBD AACBD
填空题
11.-2;12.![]() ;13.
;13.![]() ;14.
;14.![]() ;15.
;15.![]() .
.
解答题
16.解:
![]()
![]() =
=![]() (2’)
(2’)
![]()
![]() =
=![]() ……………………… (4’)
……………………… (4’)
=![]() ………………………………(7’)
………………………………(7’)
=0 . ……………………………………………(8’)
![]()
![]()
![]() .
………………………………………… ( 9’)
.
………………………………………… ( 9’)
17.解:(1)![]() 时,
时,![]() 的最大值为
的最大值为![]() . …………………………(2’)
. …………………………(2’)
![]() 时,
时,![]() 的最大值为
的最大值为![]() . …………………………(4’)
. …………………………(4’)
(注:![]() 只要有就不扣分,没有则扣一分)
只要有就不扣分,没有则扣一分)
(2)![]() .
.
![]() ,解得
,解得![]() …………………………(7’)
…………………………(7’)
∵当![]() 时,方程为
时,方程为![]() 恰有一根-1在[-1,1]内.
恰有一根-1在[-1,1]内.![]()
∵当![]() 时,方程为
时,方程为![]() 恰有一根1在[-1,1]内.
恰有一根1在[-1,1]内.![]()
综上![]() .
…………………………………… (9’ )
.
…………………………………… (9’ )
(3)答案:![]() ,x0
,x0![]() (2.625,2.75).
(2.625,2.75).![]() 其中求近似解占2分,写
其中求近似解占2分,写![]() 所在区 间占 1分(参看课本P81习题2.5第3题的解答).
所在区 间占 1分(参看课本P81习题2.5第3题的解答).
18.解:(1)根据题给图形,∵角![]() 是以
是以![]() 为始边
为始边![]() 为终边的角,
为终边的角,
∴可设![]() 由
由![]() 在
在![]() 内所转过的角为
内所转过的角为![]()
可知:以![]() 为始边,
为始边,![]() 为终边的角应为
为终边的角应为![]()
∴点P的纵坐标为![]() …………………………………(2’)
…………………………………(2’)
则:Z=![]() ………………………………………(4’)
………………………………………(4’)
上式中,当t=0时,z=0![]() 又
又![]()
![]() .
.
故所求的函数关系式为:z=![]() . ………………… (6’)
. ………………… (6’)
(2)到达最高点时,z=![]()
![]() .
.
![]() 取
取![]() .故点
.故点![]() 第一次到达最高点需要5.625(s).
…………………………………………(8’)
第一次到达最高点需要5.625(s).
…………………………………………(8’)
19.(1)答案![]() .
…………………………………………(3’)
.
…………………………………………(3’)
(2)简证:设![]()
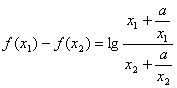 .
.
=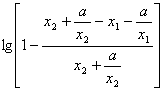 =
=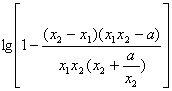 <0
<0![]()
![]() 在
在![]() 为增函数.
……………………………………………(8’)
为增函数.
……………………………………………(8’)
(3)由(2)的解答知:![]() 时,
时,![]() 取得最小值,
取得最小值,
![]() min=
min=![]() .
………………………………………(11’)
.
………………………………………(11’)