向量概念及线性运算
习题课
班级 姓名 学号 年级 学科
1．设
，
为已知向量，且
，则
等于
（ ）
A．
B．
C．
D．
2．已知
，
，则向量
与
（ ）
A．一定共线 B．一定不共线
C．仅当与共线时共线 D．仅当=时共线
3．若
，
，则
的值为
( )
A．
B．
C．
D．
4．
、
、
为非零向量，、
为实数，则命题：
①
、共线；
②
；
③、、在一个平面内
．其中真命题的个数为
（ ）
A．0 B．1 C．2 D．3
5．已知
，
，
，且
，
则
．
6．点P在线段MN上，且
，则
．
7．、为两个不共线的向量，且
，
，
，若A、B、D三点共线，则
=
．
8．已知向量
，
，
（、是不共线的向量），问
与是否共线？证明你的结论．
9．设、为两个不共线的向量，
， 
，
，求证：四边形ABCD是梯形．
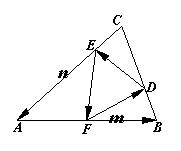
10．设D，E，F分别是△ABC的边BC，CA，AB上的点，且
，
，
．若记
，
，试用
，
表示
，
，
．
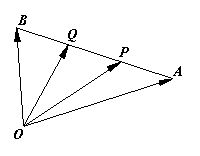
11．（1）如图，设点P，Q是线段AB的三等分点，若
，
，试用
，
表示向量
，
．
（2）在（1）中，当点P，Q三等分线段AB中，有
．如果点
是AB的
等分点，你能得出什么结论？请证明你的结论．
（3）条件同（1）（2），试用试用，表示向量
（
）．
三、方法小结：