2．2．2 向量的减法
班级 姓名 学号 年级 学科
一、概念回顾（认真阅读课本第65,66,67,68页，回答下面问题）
1． 叫做向量的减法；
从几何图形上看，向量减法同样有 法则和 法则。
2．与“减去一个数等于加上这个数的相反数”类比，可得：
。
二、理解与应用
1．化简
所得结果是
（ ）
A．
B．
C．
D．
2．在
ABC中，
，则
的值为 （ ）
A．0 B．1 C．
D．2
3．设
和
的长度均为6，夹角为 120
，则
等于 （ ）
A．36 B．12 C．6 D．
4．下面四个式子中不能化简成
的是
（ ）
A．
B．
C．
D． 
5．在
ABCD中，
，
，则
，
。
6．在=“向北走20km”，=“向西走15km”，则
=_________，
与的夹角的余弦值=______________。
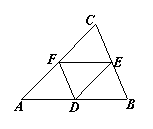
7．如图，D、E、F分别是ABC边AB、BC、CA上的
中点，则等式：
①
②
③
④
其中正确的题号是__________________
8．已知
、
是非零向量，指出下列等式成立的条件：
①
成立的条件是_________________________；
②
成立的条件是_________________________；
③
成立的条件是 _________________________；
④
成立的条件是_________________________。
9．“任何一个向量都可以表示成两个不共线的向量的和”这句话如果正确请画图说明，如果不正确，请举出反例。
10．当两个向量，不共线时，求证：
（1）
；（2）
。
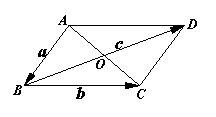
11．如图，O是ABCD的对角线AC与BD的交点，若，
，
，证明：
。
12．已知长度相等的三个非零向量、、
满足
，
求每两个向量之间的夹角。
三、方法小结：