高一级数学第二学期期中考试
科试卷
考试时间：120分钟 满分150分 命题教师：WHT
一、选择题：共10小题，每题5分，共50分。每题的四个选项中，只有一项是符合题目要求的，选出该选项的字母标号，填入答题卡相应的位置.
(1)
等于
(A)
(B)
(C)
(D)
(2) 下列两个变量之间的关系是相关关系的是
(A)正方形的面积与边长 (B)角的弧度数和它的正弦值
(C)广告的支出经费与商品的销售收入 (D)出租车的车费与行驶的里程数
(3)某市通用电器厂从已编号(1~50)的50支日光灯成品中随机抽取5支进行质量检验，用每部分选取的号码间隔一样的系统抽样方法确定选取5支的编号可能是
(A)3,9,15,21,27 (B) 6,11,16,21,26 (C)5,15,25,35,45 (D)9,17,25,33,41
(4) 十进制的数2006化为5进制的数，这个数从右往左数第一位数字是
(A) 1 (B) 2 (C) 3 (D) 4
(5)若角
与
终边互为反向延长线，则与的关系一定是
(A)
(B)
(C) 
(D)
(6)右图是BASIC语言的一个程序，执行后的输出结果是
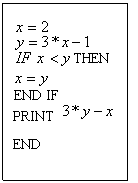
(A) 4 (B)10
(C)
(D) 13
(7)已知
，则
等于
(A) 
(B) 
(C)
(D)
(8)甲、乙两人约定：从装有2个红球和2个白球的袋中无放回地取两次球(四个球除颜色不同外，大小外型相同)，若取出的两球同色，则甲胜，若异色则乙胜.则
(A)甲获胜概率大 (B)乙获胜的概率大
(C)两人获胜的概率相等都为 (D) 两人获胜的概率相等但不等于
(9)将一条长为5cm的绳子随机地切成两段，A表示事件“所切两段都不小于1cm”，则A事件的概率是
(A)
(B)
(C)
(D) 
(10)若
、
是锐角三角形的两个内角，则点
在
(A)第一象限 (B)第二象限 (C) 第三象限 (D)第四象限
第二学期期中考试
高一级数学科试卷
考试时间：120分钟 满分150分 命题教师：WHT
| 甲卷得分 | 乙卷得分 | 总 分 |
一、选择题：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题：本大题共4小题，每小题5分，共20分.
(11)
2弧度的圆心角所对的弧长为6，则这个圆心角所夹的扇形的面积是________
(12) 某杂志《自测健康状况》报道中，自测血压结果与相应年龄的的统计数据如下表。观察表中的数据特点，用适当的数填入表中的空白(_____)处.
| 年龄(岁) | 30 35 40 45 50 55 60 65 |
| 收缩压(水银柱：毫米) | 110 113 116 119 122 125 (___) 131 |
| 舒张压(水银柱：毫米) | 71 74 73 76 77 80 (___) 84 |
(13)函数
(
)的最大值是_________，取得最大值时自变量
的取值集合是____________________
(14) 设函数f
(x)的图象与直线x =a，x =b及x轴所围成图形的面积称为函数f(x)在[a，b]上的面积，已知函数y＝sin(nx)在[0，
]上的面积为
（n∈N*
），（i）y＝sin3x在[0,
]上的面积为 ；（ii）y＝sin（3x－π）＋1在[
，
]上的面积为 .
三、解答题：本大题共6小题，共80分。解题应写出文字说明、证明过程或演算步骤。
(15)(12分，允许用计算器) 某地的海水养殖鱼身体吸收汞，汞的含量若超过体重的1.00ppm(百万分之一)时就会对人体产生危害。在15条鱼的样本中发现的汞含量是：
0.95 1.16 0.98 1.37 1.02 1.43 1.16 0.72
1.20 1.14 0.82 1.35 1.29 1.26 1.31
| 0.7 | 2 |
| 0.8 | 2 |
| 0.9 | 5 8 |
| 1.3 | 1 5 7 |
| 1.4 | 3 |
①用前两位数作为茎，补完样本数据的茎叶图(右图)，并简要描述样本的汞含量分布特点。
②求出样本数据的平均数
和标准差
.(精确到0.01)
③求含汞量在
与
之间的鱼所占百分比.
(16)(14分)
已知角终边上有一点M(-3,6)
①求
的值
②化简：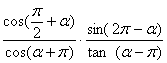
，并求该式的值.
(17)(14分)问题：求使不等式
成立的最小自然数
.
请你设计一个算法解决这个问题。要求：简要说明你的算法思路，后画程序框图表示你的算法，无须用程序语言写程序.
(17)(12分) 刘老师手中拿着红心与方片两种花色的扑克牌共16张，其中红心的牌号两两不同，方片的牌号也两两不同。现让你从中不放回地任抽取两张，若你取得同种花色的概率是，问老师手中红心与方片的牌相差几张？
(参考定理：从个不同的元素中任取出两个不同的元素组成一组，则不同的可能组合共有
种)
(19)(14分)是否存在实数
与
，使
的值与无关，且恒等于1，若存在，求出
的值，若不存在，说明理由.
(20)(14分)已知函数
的定义域是Ｒ，对任意实数，均有
与
成立，对
，用
表示区间
，当
时,
.
①证明：是周期函数
②试求在上的解析式
③过坐标系原点随机任作一条倾斜角为锐角的直线，求该直线与函数
的图象交点多于
个的概率．