高一数学同步期末测试题
一、选择题：（本大题共10小题，每小题5分，共50分）
1．已知 f ( x ) = 
+ 1 ，则 f ( 0 ) = （ ）
A．－1 B．0 C．1 D．2
2．已知等差数列
中，
，则
的值是 （ ）
A．15 B．30 C．31 D．64
3．函数
的定义域为 （ ）
A．
B．（－2，3） C．
D．
4．已知p：
则p是q的 （ ）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
5．集合A={x
} B={
} C={
}又
则有 （ ）
A．（a+b）
A B．(a+b) B
C．(a+b) C D． (a+b) A、B、C任一个
6．函数
（其中n∈N*），K是
的小数点后第n位数，
则
的值等于 （ ）
A．1 B．2 C．4 D．6
7．如果数列
的前n项和
，那么这个数列 （ ）
A．是等差数列但不是等比数列； B．是等比数列不是等差数列；
C．既是等差数列又是等比数列； D．既不是等差数列又不是等比数列．
8．已知等差数列的公差为2,若
成等比数列, 则
= （ ）
A．–4 B．–6 C．–8 D． –10
9．
是各项均为正数的等比数列，
是等差数列，且a6=b7，则 （ ）
A．
B．
C．
D．
10．某种电热水器的水箱盛满水是200升，加热到一定温度可浴用．浴用时，已知每分钟放水34升，在放水的同时注水，
分钟注水
升，当水箱内水量达到最小值时，放水自动停止．现假定每人洗浴用水65升，则该热水器一次至多可供 （ ）
A．3人洗澡 B．4人洗澡 C．5人洗澡 D．6人洗澡
二、填空题：本题共4小题，每小题4分，共16分．把答案填在题中的横线上．
11．有a、b、c三本新书，至少读过其中一本的有18人，读过a的有9人，读过b的有8人，读过c的有11人，同时读过a，b的有5人，读过b，c的有3人，读过c，a的有4人，那么a，b，c全部读过的有______________人.
12．对于任意的实数
，不等式
恒成立，则实数
的取值范围为______________.
13．若数列{an}满足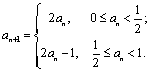
若
，则
的值为_____ __.
14．设数列
的前
项和为
（
*）.
关于数列有下列三个命题：
（1）若既是等差数列又是等比数列，则
；
（2）若
，则是等差数列；
（3）若
，则是等比数列.
这些命题中，真命题的序号是 .
三、解答题:本大题共5小题，共64分．解答应写出必要的文字说明、证明过程及演算步骤．
15．已知
是定义在R上的奇函数，当
(12分)
（1）求函数；（2）解不等式<1.
16．已知奇函数，偶函数
满足
求证：
． (12分)
17．设各项均为正数的数列
的前n项和为
，对于任意的正整数n，都有下面的等式成立. 
（1）求
；（2）求证
．(12分)
18．在等差数列中，公差
的等比中项.已知数列
成等比数列，求数列
的通项
(14分)
19．已知函数f ( x ) 满足
，b ≠0，f ( 2 ) = －1，
且f ( 1－x ) = － f ( x +1 )对两边都有意义的任意x都成立． (14分)
（1）求f ( x )的解析式及定义域；
（2）写出f ( x )的单调区间，并用定义证明在各单调区间上是增函数还是减函数？
（3）若y = f ( x ) 与
交于A，B两点，O为坐标原点，求三角形OAB的面积．
高一数学同步期末测试题答案
一、选择题
1．D 2．A 3．C 4．A 5．B 6．B 7．B 8．B 9．B 10. B
二、填空题
11．２ 12．（－∞，3） 13．
14．（1）、（2）、（3）.
三、解答题
15．（1）由题意，得
|
|
|
．
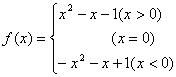
综述
．
16． 
∵是奇函数，是偶函数，
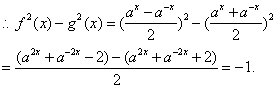
17． (1)当n=1时，
.
（2）当
时，
，
．
当n=1时，也符合
，
．
18．依题设得
，∴
，整理得d2=a1d，
∵
得
所以， 由已知得d，3d，k1d，k2d，…，kndn…是等比数列.
由
所以数列 1，3，k1，k2，…，kn，…
也是等比数列，首项为1，公比为
等比数列
，
即得到数列
19． （1）由
，
，∴x ≠ c，得
，
由
，得
，∴
.
由
，得 
， 即
.
因此
， 其定义域为
.
（2）
在 (－∞，1) 和（1，+∞）上都是增函数.
下面证明在（1，+∞）上是增函数.
设x1 ，x2∈（1，+∞），且x1 ＜ x2 ，
则 
，
∴
，
∴在（1，+∞）上是增函数.
同理可证在(－∞，1)上也是增函数.
（3）由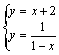
得点A，B的横坐标分别为
，
.
又直线y = x + 2与y轴的交点为P (0，2 ) ，
∴
.