浙江五校联考
高一数学(下)期中考试卷
考试时间100分钟,满分100分 2005.4
一、选择题:本在题共12个小题,每小题3分,满分36分。在每小题的四个选项中,只有一项符合要求。
1.下列命题正确的是( )
A.小于900的角是锐角; B.钝角是第二象限角;
C.第一象限角一定不是负角; D.第二象限角必大于第一象限角。
2.![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.下列不等式中,正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
4.函数![]() 的奇偶性是 ( )
的奇偶性是 ( )
![]() A.奇函数 B.偶函数 C.既是奇函数又是偶函数 D.非奇非偶函数
A.奇函数 B.偶函数 C.既是奇函数又是偶函数 D.非奇非偶函数
5.函数![]() 的定义域为( )
的定义域为( )
A.[![]() -
-![]() ,
,![]() +
+![]() ]
B.(
]
B.(![]() -
-![]() ,
,![]() +
+![]() )
)
C.[![]() +
+![]() ,
,![]() +
+![]() ]
D.(
]
D.(![]() +
+![]() ,
,![]() +
+![]() ) (以上k
) (以上k![]() Z)
Z)
6.函数![]() 的周期
的周期![]() ,那么常数
,那么常数![]() 为( )
为( )
A.![]() B.2 C.
B.2 C.![]() D.4
D.4
7.若![]() 则
则![]() 的值为( )
的值为( )
A.![]() B.1 C.
B.1 C.![]() D.0
D.0
8.把函数![]() 的图像横坐标压缩为原来的
的图像横坐标压缩为原来的![]() (纵坐标不变),再将所得的图像向左平移
(纵坐标不变),再将所得的图像向左平移![]() ,得到的函数( )的图像。
,得到的函数( )的图像。
A.![]() B.
B.![]()
C.![]() D.
D.![]()
9.已知函数![]() 对任意
对任意![]() 都有
都有![]()
则![]() 等于( )
等于( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
10.若点![]() 在第一象限,则在
在第一象限,则在![]() 内
内![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
11.已知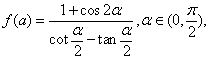 则
则![]() 取得最大值时
取得最大值时![]() 的值为(
)
的值为(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
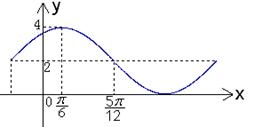 12.已知函数
12.已知函数![]() 的一部分图象如右图所示,如果
的一部分图象如右图所示,如果![]() , 则( )
, 则( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
![]() 五校联考高一数学(下)期中考试卷
五校联考高一数学(下)期中考试卷

一、选择题:本在题共12个小题,每小题3分,满分36分。在每小题的四个选项中,只有一项符合要求。
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题:本大题共4小题,每小题4分,共16分。把答案填在题中横线上。
13.计算![]() =___________
=___________
14.若扇形的周长是8cm,面积4cm2,则扇形的圆心角为_________rad
15.若![]() 则
则![]() ___________________;
___________________;
16.给出下列命题:
①函数![]() 是偶函数;
是偶函数;
②函数![]() 在闭区间
在闭区间![]() 上是增函数;
上是增函数;
③直线![]() 是函数
是函数![]() 图象的一条对称轴;
图象的一条对称轴;
④将函数![]() 的图象向左平移
的图象向左平移![]() 单位,得到函数
单位,得到函数![]() 的图象;
的图象;
其中正确的命题的序号是: ;
三、解答题:本大题共6小题,共58分。解答应写出文字说明,证明过程或演算步骤。
17.(本题8分)化简 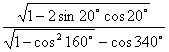
18.(本题8分)已知![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的值
的值
19.(本题10分)已知锐角三角形ABC中,![]()
(1) 求证![]() ; (2) 求
; (2) 求![]() 的值;
的值;
20.(本题10分)已知函数![]()
(1)当![]() 时,求
时,求![]() 的单调递增区间;
的单调递增区间;
(2)当![]() 且
且![]() 时,
时,![]() 的值域是
的值域是![]() 求
求![]() 的值.
的值.
|

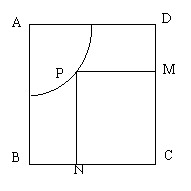 21.(本题12分)如图正方形场地ABCD边长为2km,在A附近已先占用以A为圆心以1km为半径的
21.(本题12分)如图正方形场地ABCD边长为2km,在A附近已先占用以A为圆心以1km为半径的答 案
一、选择题:本在题共12个小题,每小题3分,满分36分。
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | C | B | A | B | C | A | C | B | B | B | C |
二、填空题:本大题共4小题,每小题4分,共16分。
13. ![]() 14. 2 15.
2005
16. ①③
14. 2 15.
2005
16. ①③
三、解答题:本大题共6小题,共58分。解答应写出文字说明,证明过程或演算步骤。
17. 解:原式=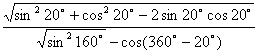 -------------------(4分)
-------------------(4分)
![]() ------------------------------------------(6分)
------------------------------------------(6分)
![]()
![]() -------------------------(8分)
-------------------------(8分)
18.解:∵![]()
∴![]() 又
又![]() ∴
∴![]() ------(2分)
------(2分)
∵![]() ∴
∴![]() 又
又![]()
∴![]() ---------(4分)
---------(4分)
∴![]()
![]()
![]() -------------(8分)
-------------(8分)
19.(1)证明:![]()
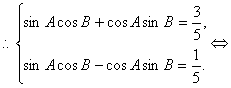 -------------(2分)
-------------(2分)
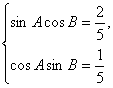 -
-
![]()
![]()
所以![]() -------------------(5分)
-------------------(5分)
(2)解析:![]() ,
,![]()
即![]() ,
------------(7分)
,
------------(7分)
将![]() 代入上式并整理得
代入上式并整理得
![]() -----------(9分)
-----------(9分)
解得![]() ,舍去负值得
,舍去负值得![]() ---------(10分)
---------(10分)
20.解:(1)![]() ---(4分)
---(4分)
由![]() 得
得![]()
![]() 当
当![]() 时,
时,![]() 的递增区间为
的递增区间为![]() -------------(6分)
-------------(6分)
(2)由![]() 得
得![]()
又![]()
![]()
由题意知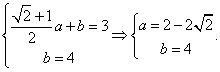 ------------------(10分)
------------------(10分)
21.解:延长NP交AD于Q,则∠QAP=![]() ,(0°≤
,(0°≤![]() ≤90°)
≤90°)
AQ=![]() ,PQ=
,PQ=![]()
∴PN=![]() ,PM=
,PM=![]() ---------(4分)
---------(4分)
∴S=PN•PM=![]() =
=![]() (6分)
(6分)
设![]() (1≤t≤
(1≤t≤![]() ),则
),则![]() =
=![]()
![]()
当t=1时,S的最大值为2km2
答:这幢楼房的最大占地面积是2km2 ------------(12分)