高一年级数学第一学期期末考试试卷
一、填空题（每小题4分，满分48分）
1、若
，则
2、设函数
的最小值为
3、函数
的单调增区间是
4、关于
的方程
的解集为
5、函数
图像的对称中心的坐标为
6、函数
的值域为
7、若函数
是奇函数，则实数
=
8、函数
在区间
上是减函数，则实数的取值范围是
9、若函数
=
的定义域为R，则实数a的取值范围
10、函数
的反函数是
11、已知定义在R上的奇函数满足
，则
12、函数在定义域
上是增函数，且满足
，
计算：
，
，……可归纳出
共4页第1页
二、选择题（每小题3分，满分12分）
13、若奇函数在
上是增函数，且最小值为2，则在
上是
（A）增函数且最小值是
（B）增函数且最大值是
（C）减函数且最小值是 （D）减函数且最大值是
（ ）
14、若
，条件甲：“函数
在R上是增函数”，条件乙：“函数
在
上是增函数”，则条件甲是条件乙的
（ ）
（A）充分非必要条件 （B）必要非充分条件
（C）充要条件 （D）既非充分也非必要条件
15、设为奇函数,当
时,
；当
时，有 ( )
（A）
（B）
（C）
（D）
16、已知函数
，若当
时，
恒成
立，则 （ ）
（A）在
上是增函数 （B）在
上是增函数
（C）在上是减函数 （D）在
上是减函数
三、解答题
17、（6分）已知函数
满足
，求
的值，并
求出相应的解析式
共4页第2页
18、（8分）设
，定义函数
，当
时，
，当
时，
，（1）在直角坐标系中作函数
的图像；（2）求函数的最小值。
解：（1） （2）
19、（8分）
且
)
(1)判断的奇偶性并证明;(2)求使的的取值范围.
共4页第3页
20、（8分）设函数
,（1）判断函数在
上的单调性；并用函数的单调性定义证明；（2）求关于的方程
在上的解。
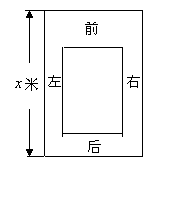
21、（10分）某科研基地计划建造一个室内面积为800平方米的矩形蔬菜温室,在温室内,沿左、右两侧与后侧内墙各保留1米宽的通道，沿前侧内墙保留3米宽的空地，设矩形温室的左侧边长为米，蔬菜的种植面积为
平方米。
（1）写出关于的函数关系式；并写出定义域；（2）求矩形蔬菜温室的最大面积，并求此时的值。
共4页第4页
上海市北郊高级中学2006学年第一学期期末考试
高一年级数学参考答案
一、填空题
1、 5 2、 -7
3、 
4、 
5、 
6、
7、 
8、 
9、 
10、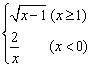 
11、 0
12、 0；2；
二、选择题
13、B 14、 C 15、C 16、B
三、解答题
17、（1）
（2）
18、（1）图略 （2）
19、（1）奇函数 （2）当
时，
；当
时，
20、（1）增函数 （2）
21、（1）
（2）当
米时，面积最大为648平方米