高一年级数学阶段性测试试卷
命题人：朱跃民 审定人：朱益民
一、
选择题（12
5分=60分）每题只有一个正确选项，填入题后表格
1、已知集合A=
，则下列各式中正确的是
（A）
A （B）
A
（C）
A （D）0A
2、设A=
，B=
，则A
B=
（A）R （B）
（C）
（D）
3、已知
，则函数
的定义域为
（A）R （B）
（C）
（D）
4、下列既不是奇函数也不是偶函数的函数是
（A）
=
（B）=
（C）=2
（D）=2
5、直线=和定义在
函数
= 的图象的公共点有
（A）0个 （B）1个 （C）2个 （D）0个或1个
6、已知
A=
，则满足条件的集合A有
（A）0个 （B）1个 （C）2个 （D）3个
7、已知=
则
（A）1 （B）5 （C）-1 （D）4
8、函数
的值域是
（A）
（B）
（C）
（D）
9、对函数
上的单调性描述正确的是
（A）增函数 （B）减函数 （C）先增后减 （D）先减后增
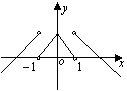10、已知函数
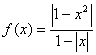，则其图象为
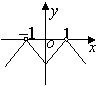
（A） （B） （C） （D）
11、已知
是集合A=到集合B=
的映射，则这样的映射共有
（A）1个 （B）2个 （C）4个 （D）6个
12、对于集合A与B，定义A*B=
，若A中有3个元素，B中有2个元素，则A*B中的元素个数为
（A）5个 （B）6个 （C）8个 （D）9个
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、
填空题（44=16分）
13、比较大小：
14、已知=
则
+
+
+
+
+
+
=
15、已知与
是定义在R上的两个不同函数
①若单调递增，单调递增，则
单调递增；
②若单调递增，单调递减，则
单调递减；
③若是偶函数，也是偶函数，则
是偶函数；
④若是奇函数，也是奇函数，则
=
是偶函数；
以上四个命题，正确的是 （请填入所有正确命题的序号）
16、有一类函数，其定义域为R，值域为
，如
。请再写出一个这样的函数
三、
解答题（512分+14分=74分）
17、已知函数
(
)，求其值域并写出单调区间（不证明）。
18、已知集合A=
，集合B=
（1）求AB （2）求AB （3）若集合C是由只属于A与B之一的元素组成的新集合，求集合C。
19、已知集合A=
，B=
，且
，试求实数值。
20、①利用指数的运算法则，解方程：
；
②定义在R上奇函数，当
时 
，求的解析式。
①
②
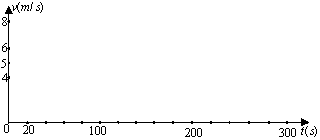
21、田径队的小刚同学在教练指导下进行长跑的训练，过程计划如下：
①起跑后，匀加速，20s后达到5m/s的速度，再匀速跑到1分钟；
②开始均匀减速，到2分钟时已经减到4m/s，再保持匀速跑1分钟；
③在40 s之内，均匀加速达到6m/s的速度，保持匀速跑20s；
④在1分钟之内，均匀加速冲刺，使最终速度达到8m/s。结束训练。
（1）在所给坐标系中画出小刚跑步的时间t(s) 与速度v(m/s)的函数图象；
（2）写出小刚进行长跑训练时，跑步速度关于时间的函数解析式。
22、已知函数
是定义在（
，1）上的奇函数，且
，
（1）确定函数的解析式
（2）用定义证明在（，1）上是增函数
（3）解不等式
（4）若10<
对所有的
都成立，求实数
的范围。