数列单元测试
一、选择题：(每小题4分,共40分)
1．已知
的三个内角分别是A、B、C，B=60°是A、B、C的大小成等差数列的（
C ）
A． 充分非必要条件 B. 必要非充分条件
C. 充要条件 D.既非充分也非必要条件
2．已知
，则
的值为 （ B ）
A．
B．
C．
D．
3．等比数列
中， 
， 
，则
值为（ B）
A．5 B．6 C．7 D．8
4．已知数列
的前n项和Sn与第n项
满足
等于（ B ）
A．
B．
C．
D．
 |
5．黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案：
则第
个图案中有白色地面砖的块数是 （A ）
A．
B．
C．
D．
6．设
是等差数列，
是其前
项的和，且
，
，则下列结论错误的是 （ B ）
A．
B．
C．
D．
与
是的最大值
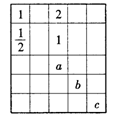
7．在如图的表格中，每格填上一个数字后，使每一横行成等
差数列，每一纵列成等比数列，则
的值为（ A ）
A．1 B．2
C．3 D．4
8．若{an}是等差数列，且a1＋a4＋a7=45，a2＋a5＋a8=39，则a3＋a6＋a9的值是（ D ）
A．39 B．20 C．19.5 D．33
9．如果数列
的前n项和
，那么这个数列 （ B
）
A．是等差数列但不是等比数列； B．是等比数列不是等差数列；
C．既是等差数列又是等比数列； D．既不是等差数列又不是等比数列．
10．已知等比数列
的首项为8，
是其前n项的和，某同学经计算得
S2=20，S3=36，S4=65，后来该同学发现了其中一个数算错了，则该数为 （ C）
A． S1 B．S2 C． S3 D． S4
二、填空题：本题共5小题，每小题5分，共25分．把答案填在题中的横线上．
11．等比数列的前项和
=
，则=_
______.
12．数列1，0，2，0，3,…的通项公式为 
13．某人为了观看2008年奥运会，从2001年起，每年5月10日到银行存入
元定期储蓄，
若年利率为
且保持不变，并约定每年到期存款均自动转为新的一年定期，到2008年将
所有的存款及利息全部取回，则可取回的钱的总数（元）为_ 
14．定义“等和数列”：在一个数列中，如果每一项与它的后一项的和都为同一个常数，那
么这个数列叫做等和数列，这个常数叫做该数列的公和。已知数列
是等和数列，且
，公和为5，那么
的值为___，且这个数列的前n项和
的计算公式为 .
15．如果
是
与
的等差中项，
是
与
的等比中项，且
都是正数，则
0 （
）
三、解答题:本大题共3小题，共35分．解答应写出必要的文字说明、证明过程及演算步骤．
16．假设你正在某公司打工，根据表现，老板给你两个加薪的方案：
（Ⅰ）每年年末加1000元； （Ⅱ）每半年结束时加300元。请你选择．(12分)
（1）如果在该公司干10年，问两种方案各加薪多少元？
（2）对于你而言，你会选择其中的哪一种？
设方案一第n年年末加薪an，因为每年末加薪1000元，则an=1000n；
设方案二第n个半年加薪bn，因为每半年加薪300元，则bn=300n；
(1) 在该公司干10年(20个半年)，方案1共加薪S10=a1＋a2＋……＋a10=55000元.
方案2共加薪T20=b1＋b2＋……＋b20=20×300＋
=63000元；
(2) 设在该公司干n年，两种方案共加薪分别为：
Sn=a1＋a2＋……＋an=1000×n＋
=500n2＋500n,
T2n=b1＋b2＋……＋b2n=2n×300＋
=600n2＋300n,
令T2n≥Sn即：600n2＋300n>500n2＋500n，解得：n≥2，当n=2时等号成立.
∴如果干3年以上(包括3年)应选择第二方案；如果只干2年，随便选；如果只干1年，当然选择第一方案.
17．设函数
,数列
的通项满足
. (12分)
（1） 求数列的通项公式； （2）判定数列{a n }的单调性.
⑴∵，又，
∴
令
，则
，∴
，
注意到，因此＝
， 
，
， ∴
即为数列的通项公式.
，可知数列是递增数列.
18．某地区发生流行性病毒感染，居住在该地区的居民必须服用一种药片预防，规定每人每天上午
时和晚上
时各服一片。现知该药片每片含药量为
毫克，若人的肾脏每
小时从体内滤出这种药的
，该药物在人体内的残留量超过
毫克，就将产生副作用. (12分)
（1）某人上午时第一次服药，问到第二天上午时服完药后，这种药在他体内还残留多少？
（2）若人长期服用这种药，这种药会不会对人体产生副作用？说明理由。
（1）设人第次服药后，药在体内的残留量为毫克，则
，
，
，即到第二天上午时服完药后，这种药在他体内还残留
毫克；
（2）由题意：
，∴
，
∴
是以
为首项，
为公比的等比数列，
∴
，
∵
，∴
，∴
。故若人长期服用这种药，这种药不会对人体产生副作用。