高一数学第一学期第一次月训试卷
一、选择题(12×5′=60′)
1、下列描述中能构成集合的是 ( )
A、![]() 的近似值 B、性格开朗的人
的近似值 B、性格开朗的人
C、接近于0的数 D、绝对值小于2的实数全体
2、下列各式中
(1)1∈{0,1,2} (2)![]() (3){0}=
(3){0}=![]()
(4)A∩B![]() A (5)A∩B∈A∪B (6)
A (5)A∩B∈A∪B (6)![]() ∈{
∈{![]() }正确的个数是( )
}正确的个数是( )
A、1个 B、2个 C、3个 D、4个
3、设p={x|x≤8},a=![]() ,则下列关系中正确的是 ( )
,则下列关系中正确的是 ( )
A、a![]() p B、a
p B、a![]() p C、{a}∈p D、{a}
p C、{a}∈p D、{a}![]() p
p
4、设A={x|x≤4,x∈N},B=![]() x|-3≤x<1,x∈Z
x|-3≤x<1,x∈Z![]() ,则A∩B=__
,则A∩B=__
A、{1,2} B、{-2,-1} C、![]() D、{0}
D、{0}
5、集合A={x|-1≤x≤2},集合B={x|x≤a},若A∩B≠![]() ,则实数a的取值范围是 ( )
,则实数a的取值范围是 ( )
A、{a|a≤2} B、{a|a≥-1}
C、{a|a>-1} D、{a|-1≤a<2}
6、下列函数![]() 与
与![]() 中表示同一函数的是 ( )
中表示同一函数的是 ( )
A、![]() 与
与![]() B、
B、![]() 与
与![]()
C、![]() 与
与![]() D、
D、![]() 与
与![]()
7、下列函数中,在(-∞,0)内是减函数的是 ( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
8、函数![]() ,在
,在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,则m= ( )
上是减函数,则m= ( )
A、-16 B、16 C、-8 D、8
9、如果奇函数f(x)在[3,7]上增函数,且有最小值5,那么在区间[-7,-3]上是 ( )
A、增函数,且最小值为-5 B、增函数,且最大值为-5
C、减函数,且最小值为-5 D、减函数,有最大值为-5
10、函数y=|x|+3的单调增区间是 ( )
A、(-∞,0) B、(-3,3) C、(0,3) D、(0,+∞)
11、已知偶函数f(x)的定义域为{x|x∈R,且x≠0},若f(x)在(0,+∞)内单调递增,则 ( )
A、f(-1)<f(-2)<f(-3) B、f(-1)<f(-3)<f(-2)
C、f(-3)<f(-2)<f(-1) D、f(-2)<f(-1)<f(-3)
12、已知函数![]() 且f(-2)=10,则f(2)=( )
且f(-2)=10,则f(2)=( )
A、-26 B、-18 C、-10 D、10
二、填空题(6×4′=24′)
13、已知![]()
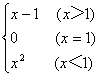 ,则f(-2)=_______,f[f(2)]=____
,则f(-2)=_______,f[f(2)]=____
14、函数![]()
![]() 的定义域为_______;函数
的定义域为_______;函数![]()
![]() 的值域为_______(都用区间表示)。
的值域为_______(都用区间表示)。
15、判断函数的奇偶性:![]()
![]() 为________,
为________,![]() 为_________
为_________
16、若![]() ,则
,则![]() =_______
=_______
17、设A={0,1,3,4},B={1,2,10,17,19},试写出一个从集合A到集合B的映射f:x→________________________
18、请构造符合条件:①是偶函数;②在区间![]() 上单调减小的一个函数:________________
上单调减小的一个函数:________________
 高一第一次月训数学试卷答题纸
高一第一次月训数学试卷答题纸
二、填空题(6×4′=24′)
13、_______ _______
14、_______ _______
15、_______ _______
16、_______
17、_______
18、_______
三、解答题(66分)
19、求值:![]() (6′)
(6′)
![]() ,试求
,试求 的值。(6′)
的值。(6′)
20、已知集合A=![]() ,
,![]() 为实数
为实数
(1) 若A是空集,求![]() 的取值集合;
的取值集合;
(2) 若A是单元素集合,求![]() 的取值集合。(12′)
的取值集合。(12′)
21、已知![]() 为定义在R上的奇函数,当x>0时,
为定义在R上的奇函数,当x>0时,![]() ,求
,求![]() 的表达式。(12′)
的表达式。(12′)
22、已知函数![]() 在定义域[1,2]内为单调减小函数,又f(1-2a)>f(4+a),求满足条件的实数a的取值集合。(12′)
在定义域[1,2]内为单调减小函数,又f(1-2a)>f(4+a),求满足条件的实数a的取值集合。(12′)
23、(应用题)某公司将进货单价为8元一个的商品按10元一个销售,每天可卖出100个,若这种商品的销售价每个上涨1元,则销售量就减少10个,若设定价为x元,销售利润为y元,
(1) 写出y关于x的函数解析式;
(2) 求销售的最大利润,并求此时的定价是多少?(12′)
24、(分析题)已知函数![]() 、c、d为实数,
、c、d为实数,![]() 、b、c不全为零)
、b、c不全为零)
1°试确定![]() 、b、c、d的值,使f(x)为偶函数;
、b、c、d的值,使f(x)为偶函数;
2°试确定一组![]() 、b、c、d的值,使f(x)为单调函数;
、b、c、d的值,使f(x)为单调函数;
3°若f(x)为奇函数,讨论![]() 、b、c、d的取值范围。(6′)
、b、c、d的取值范围。(6′)