高一数学第一学期期中调研试卷
一、选择题：（本大题共12小题. 每小题5分，共60分.）
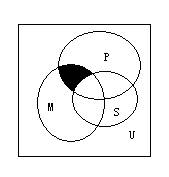1.如图,
是全集，
是的三个子集，则阴影部分所表示的集合是（
）
A.
B.
C.
D.
2.若
，
，
，则（
）
A.
B.
C.
D.
3.下列四组函数中，表示同一函数的是（ ）
A.
B.
C.
D.
4.函数
的定义域是（
）
A.
B. 
C.
D.
5.若
，则
的值为（
）
A.
B.4
C.1
D.4或1
6.设
，则
的值为（ ）
A.
B.
C.
D.
7.方程
的解所在的区间为（ ）
A.
B.
C.
D. 
8.函数
的单调递增区间是（ ）
A.
B.
C.
D.
9.函数
的图象是由
的图象经过（ ）变换得到的
A.先向左平移2个单位，再向上平移2个单位
B.先向左平移2个单位，再向下平移2个单位
C.先向右平移2个单位，再向上平移2个单位
D.先向右平移2个单位，再向下平移2个单位
10.某商品零售价2002年比2001年上涨
，欲控制2003年比2001年只上涨
，则2003年应比2002年下降（ ）
A.
B.
C.
D.
11.设偶函数
的定义域为R，当
时，是增函数，则
，
，
的大小关系是（ ）
A.
B.
C.
D.
12.已知方程
的两根为
，则
（ ）
A.
B.
C.6
D. 
二、填空题：（共6小题.每小题4分，共24分）
13.函数
的定义域为
.
14.已知集合
，
，从
到
的不同的映射有
个.
15.设
，则
的大小关系为
.
16.函数
在
上是减函数，则
的取值范围是
.
17.函数
在
上最大值比最小值大
，则
的值为
.
18.王老师给出一个函数
，四个学生甲、乙、丙、丁各指出了这个函数的一个性质.甲：对于
R，都有
；
乙：在
上是减函数；
丙：在
上是增函数；
丁： 
不是函数的最小值.
现已知其中恰有三个说得正确，则这个函数可能是 （只需写出一个这样的函数即可）.
三、解答题：（共5小题，共66分）
19.（本小题共12分）求
的值.
20.（本小题共13分）设
，求函数
的最大值和最小值.
21.（本小题共13分）若光线通过一块玻璃，其强度要损失.把几块这样的玻璃重叠起来，设光线原来的强度为
，通过
块玻璃后强度为
.
（1）写出关于的函数关系式；
（2）至少通过多少块玻璃后，光线强度减弱到原来的
以下？（
）
22.（本小题共14分）已知函数
.
（1）用分数函数的形式表示该函数；
（2）画出该函数的图象；
（3）写出该函数的定义域、值域、奇偶性、单调区间.
23.（本小题共14分）已知函数
是奇函数.
（1）求实数的值；
（2）判断函数在
上的单调性，并给出证明；
（3）当
时，函数的值域是，求实数与
的值.