
 高一数学第一学期期终复习测试(二)
高一数学第一学期期终复习测试(二)
考试时间100分钟,满分100分
| 题号 | 一 | 二 | 三 | 成绩 | ||||
| 得分 | ||||||||
一、填空题(每个4分,共40分)
1.若不等式![]() 的解集为
的解集为![]() 那么
那么![]() ____
____
2.![]() ,则
,则![]() __________
__________
3.已知函数![]() ,则
,则![]() _______
_______
4.函数![]() 的定义域为A,函数
的定义域为A,函数![]() 的定义域为B,若B
的定义域为B,若B![]() A, 则实数a的取值范围
.
A, 则实数a的取值范围
.
5.若函数![]() 的图象不经过第一、三象限,写出一组满足的条件
的图象不经过第一、三象限,写出一组满足的条件![]() 是
是
6.一种专门占据内存的计算机病毒,开机时占据内存![]() ,然后每3分钟自身复制一次,复制后所占内存是原来的2倍,那么开机后经过 分钟,该病毒占据
,然后每3分钟自身复制一次,复制后所占内存是原来的2倍,那么开机后经过 分钟,该病毒占据![]() 内存.(
内存.(![]() )
)
7.在里氏地震震级中,地震强度级数M与地震时岩石释放出的弹性波能量E之间有关系式lgE=4.8+1.5M,地震时里氏6级的地震所发出的弹性波能量是4级地震的_____倍.
8.关于x的方程![]() ,只有负根而无正根,则a的取值范围是_________
,只有负根而无正根,则a的取值范围是_________
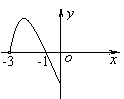 |
9.如果![]() 是定义在
是定义在![]() 上的偶函数,且当
上的偶函数,且当![]() 时,
时,
![]() 的图象如图所示,那么不等式
的图象如图所示,那么不等式![]() 的解集为 ________.
的解集为 ________.
10.已知函数![]() 具有性质:
具有性质:![]() ,请你再构造一个具有性质“
,请你再构造一个具有性质“![]() ”的一个函数(不是常值函数)_______ _ .
”的一个函数(不是常值函数)_______ _ .
二、选择题(每个3分,共12分)
11.如果![]() ,
,![]() ,那么“
,那么“![]() ”是“
”是“![]() ”的……………………………………………………………….( )
”的……………………………………………………………….( )
A.充分条件但非必要条件 B.必要条件但非充分条件
C.充分必要条件 D.非充分条件也非必要条件
12.在某一函数![]() 图象上任取两点,若这两点纵坐标的差与相对应的横坐标的差之比恒正,则此函数的单调性为……………………( )
图象上任取两点,若这两点纵坐标的差与相对应的横坐标的差之比恒正,则此函数的单调性为……………………( )
A.减函数; B.增函数;
C.先减后增; D.不确定
13.如果奇函数![]() 在区间[3,7]上是增函数,且最小值为5,那么
在区间[3,7]上是增函数,且最小值为5,那么![]() 在[-7,-3]上是……………………………………………………( )
在[-7,-3]上是……………………………………………………( )
A.增函数且最小值为-5 B.增函数且最大值为-5
C.减函数且最小值为-5 D.减函数且最大值为-5
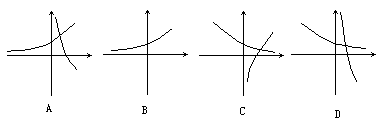
14.已知![]() ,若
,若![]() ,则
,则![]() 与
与![]() 在同一坐标系内的图象可能是…………………… ( )
在同一坐标系内的图象可能是…………………… ( )
三、解答题:(10+6+6+6+10+10=48分)
15.解下列方程
(1)![]() (2)
(2)![]()
16.若函数![]() 的图象关于
的图象关于![]() 对称
对称
求函数的最大值和最小值
17.函数![]()
(1) 判断函数的奇偶性;
(2) 写出函数的单调递增区间(不必证明);
18.已知函数![]()
(1) 若![]() ,求
,求![]() 的值;
的值;
(2) 若![]() 为常数,且
为常数,且![]() ,试讨论方程
,试讨论方程![]() 的解的个数。
的解的个数。
19.已知集合A满足:![]()
判断![]() 以及
以及![]() 是否属于集合A,说明理由;
是否属于集合A,说明理由;
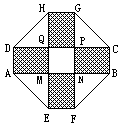
20.某小区要建一座八边形的休闲小区,它的主体造型的平面图是由二个相同的矩形ABCD和EFGH构成的面积为200平方米的十字型地域。计划在正方形MNPQ上建一座花坛,造价为每平方米4200元,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为每平方米210元,再在四个空角上铺草坪,造价为每平方米80元。
(Ⅰ)设AD长为x米,总造价为S元,试建立S关于x的函数关系式;
(Ⅱ)当x为何值时S最小,并求出这个最小值。
参考答案
一、填空题(每个2分,共28分)
1.0;
2.![]() ;
3.
;
3.![]() ;
4.
;
4.![]() ;
;
5.不唯一,只需满足![]() 即可; 6.45;
7.1000;
即可; 6.45;
7.1000;
8.![]() ; 9.
; 9.![]() ; 10.不唯一
; 10.不唯一![]() ,
,![]() 等
等
一、选择题
11.B; 12.B; 13.A; 14.D;
二、解答题
15.解(1)![]() .......................................1分
.......................................1分
![]() ...................................................1分
...................................................1分
化简![]() ............................................1分
............................................1分
解得![]() (舍去)......................................1分
(舍去)......................................1分
经检验![]() 是原方程的解......................................1分
是原方程的解......................................1分
(2)设![]() ,原方程可化为
,原方程可化为![]() ....................1分
....................1分
解得![]() (舍去)......................................2分
(舍去)......................................2分
![]() ,
,![]() ............................................2分
............................................2分
16.解:![]()
![]() 对称轴方程为
对称轴方程为![]() ,得到
,得到![]() ....................2分
....................2分
![]()
![]() ,
,![]() ..........................................1分
..........................................1分
![]()
![]() .................................1分
.................................1分
![]()
![]() 时,
时,![]()
![]()
![]() 或6时,
或6时,![]() ................................2分
................................2分
17.解:(1)函数的定义域![]() ,关于原点对称..................1分
,关于原点对称..................1分
![]() ,所以函数
,所以函数![]() 是偶函数........3分
是偶函数........3分
(2)函数的递增区间是![]() 和
和![]() ..........................2分
..........................2分
函数的递减区间是![]() 和
和![]() ...............................2分
...............................2分
18.解(1)![]() 和
和![]() ....................................2分
....................................2分
(2)![]() 时方程两解......................................2分
时方程两解......................................2分
![]() 时方程一解......................................2分
时方程一解......................................2分
![]() 时方程无解..........................................2分
时方程无解..........................................2分
19.![]() .........................................2分
.........................................2分
设![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() 在定义域内单调递增,................2分
在定义域内单调递增,................2分
![]() ,即
,即![]() ,
,![]() .............................2分
.............................2分
设![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() 在定义域内单调递增,...............................2分
在定义域内单调递增,...............................2分
![]()
![]() ,即
,即![]() ,
,![]() ............................2分
............................2分
20.(1)AM=y米,AD=x米,则![]() ,
,![]() ...........2分
...........2分
由题意得![]()
![]()
![]() ...........4分,其中定义域1分
...........4分,其中定义域1分
(2)![]()
当且仅当![]() 时取等号,此时
时取等号,此时![]() ,
,![]() .............................................4分
.............................................4分