三角函数综合测试
一、选择题：（每小题4分，共48分）.
1．若角α与角β的终边关于x轴对称，则α=（ ）.（其中k∈Z）.
A、
B、2k
-β C、(2k+1) -β D、2k+β
2．若
，且α是第三象限角，则csc(α-7)=（ ）.
A、
B、
C、-2 D、2
3．
和
分别是
的正弦线和余弦线，则有（ ）.
A、MP<OM<0 B、MP<0<OM C、OM<MP<0 D、OM<0<MP
4．下列结论正确的是（ ）.
A、
B、
C、
D、
5．cos275°+cos215°+cos75°cos15°=（ ）.
A、
B、
C、
D、
6．若
，则
=（ ）.
A、
B、
C、5 D、-5
7．函数
是（ ）.
A、周期为2π的奇函数 B、周期为π的奇函数
C、周期为2π的偶函数 D、周期为π的偶函数
8．
=（ ）
A、-1 B、
C、-2 D、2
9．函数f(x)=sinx+cosx图象的一条对称轴方程是（ ） .
A、
B、x=0 C、
D、
10．函数
定义域是（ ）（其中k∈Z),
A、
B、
C、
D、
11．若函数
在同一个周期内的
处取得最大值
，在
处取得最小值，则函数的解析式是（ ）.
A、
B、
C、
D、
12．若x∈[0,π]，则函数y=sinx-cosx的值域为（ ）.
A、
B、[-1，1] C、
D、[-1，
]
二、填空题：（每小题4分，共20分）
13．若角α是第二象限角，则点(sinα, cosα)在第_______象限.
14．若
，则sin3x-cos3x=______.
15．tan19°+tan26°+tan19°tan26°=_______.
16．函数
的单调减区间是________.
17．若
且
.则sin2x=_________.
三、解答题：
18．（本小题10分）计算：cos271°+cos71°cos49°+cos249°
19．（本小题10分）
已知：ΔABC中，
， 求证：sinA+sinC=2sinB
20．（本小题12分）
已知：
（1）求：f(x)的最大、最小值，及相应的x的值；
（2）求：f(x)的最小正周期；
（3）写出f(x)的图象是由y=sinx的图象如何变换得到的.
参考答案：
一、选择题：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | B | D | D | C | A | B | C | A | A | B | D |
解析：5.
∴原式＝
6．提示：把已知两式按两角和差的正弦公式展开，把两个展开式分别相加、相减，所得两式在相除。
8．
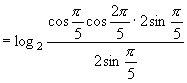
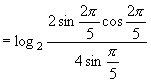
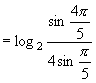
二、填空题：
| 13 | 四 | 14 |
|
| 15 | 1 | 16 |
|
| 17 |
|
|
|
三、解答题：
18．解：cos271°+cos71°cos49°+cos249°
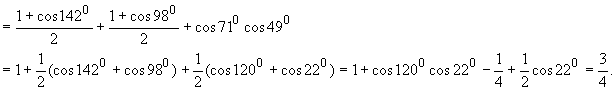19. 降次，利用sin(A+C)=sinB.
20. 
(1)
;
(2) T=