2004-2005学年度上期重庆市部分区县联合考试
高一数学试题
一、选择题（每小题5分，共60分）
1.集合
，
则M与N的关系是（ ）
A. 
B. 
C. 
D. 
2.函数
的定义域是（
）
A. 
B. 
C. 
D. 
3.若a、b、c成等比数列，则函数
的图象与x轴的交点个数为（
） A.
0
B.
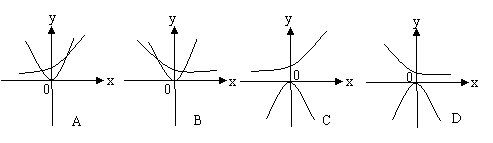4.当时
，函数
与
的图象只可能是（
）
5.给出命题：“已知a、b、c、d是实数，若
则
”。对其原命题、逆命题、否命题、逆否命题而言，真命题有（ ）
A. 1个 B. 2个 C. 3个 D. 4个
6.在等差数列
中
，
，那么数列的通项公式为（
）
A. 
B. 
C. 
D. 
7.已知
，则下列结论正确的是（
）
A. 
B. 
C. 
D. 
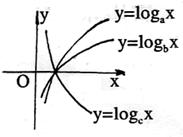
8.由图可推得a、b、c的大小关系是（ ）
A. 
B.
C. 
D.
9.已知集合
，
，
且
，则实数a的取值范围是（ ）
A. 
B.
C.
D.
10.在3与9之间插入两数，使前面三个数成等比数列，后面三个数成等差数列，则这两个数之和为（ ）
A. 
B.
C.
D.
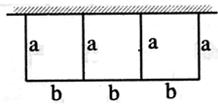11.入图，一批材料可以建成
A.
C.
12. 拟定从甲地到乙地通话m分钟的电话费（单位：元）由
给出，其中
，
是大于或等于m的最小整数（如：
）则从甲地到乙地通话5.5分钟的话费为（ ）
A. 3.71
B.
二、填空题（每小题4分，共16分）
13.已知集合
是从A到B的一个映射，若
，则B中元素3的原象为
14.计算
=
15.当
时，函数
的值域是
16.对于下列条件：① 数列的通项公式是关于n的一次函数
② 数列的前n项和
（a、b是常数）
③ 数列对任意
均有
（d是常数）
④ 数列对任意均有
其中可作为使成等差数列的充要条件的是
（填上正确的序号）
三、解答题（74分）
17.（每小题6分，共12分）（1）计算：
（2）求数列
，
，
，
，…，
，…的前n项和
18.（本题12分）已知
，集合
求：（1）
；（2）
；（3）
19. （本题12分）已知函数
（1）求函数
的反函数
（2）证明：在
上为减函数
20. （本题12分）设集合
，若
，求实数p的取值范围。
21. （本题13分）对于函数
，若存在实数
，
使成立，则称为的不动点。
（1）
时，求函数的不动点；
（2）若对于任何实数b,函数恒有两个相异的不动点，求实数a的取值范围；
（3）在（2）的条件下，若
，且
、
是的两个不动点，求
的最小值。
22. （本题13分）某渔场原有鱼2万斤，所养鱼的重量第一年的增长率为200%，以后每年的增长率都是前一年的一半，问：
（1）饲养三年后的鱼的重量是多少？
（2）如果因为环境污染，每年损失重量10%，那么经过多少年后鱼的重量开始减少？