郴州市一中高一阶段性测试数学试卷
（题量：共22题，满分：150分，时间：120分钟）
一、选择题(共10小题每小题5分，共50分，请将正确的选项填在本题后答题卡上)
1．已知全集
，集合
，
，则
∩B等于
A．
B．
C．
D．
2. 巳知映射
，则( 4，3)在f下的原象是
A. (10，5) B (2，1) C . (2，-1) D . (3，4)
3. 函数y = f( x )的定义域为
，且对定义域内的任意x，y都有f(
xy )=f( x )+f( y )，且f( 2 ) = 1，则
的值为
A
. 1
B . 
C. - 2
D . 
4. 函数f( x )在R上单调递减，且f( m2 ) > f( -m )，则m的取值范围是
A.
B. C.
D. 
5. 设y = f( x )定义在R上且f(-x)=f(x)对一切x恒成立，且当
时，
，则在上f( x )的表达式为
A. 
B. 
C
. 
D.
6．已知
，其中
，则下列不等式成立的是
A．
B．
C．
D．
7．已知数列{an}的前n项和为Sn=3n2-2n，设由
构成的数列为
，
则的通项公式为
A. 
B. 
C. 
D . 
8．将进货单价为80元的商品按90元一个出售时，能卖出400个，根据经验，
该商品若每个涨(降)1元，其销售量就减少(增加)20个，为获得最大利润，售价应定为
A．92元 B．94元 C．95元 D．88元
9. 在等差数列
中，
是方程2x2 – x – 7 = 0的两根，则
A
. B. 
C
. 
D. 
10．若
A．关于直线y=x对称 B．关于x轴对称
C．关于y轴对称 D．关于原点对称
| 题号 | 1 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
二、填空题（共6小题每小题4分，共24分）
11．已知等差数列中，a7=9,则S13=__________
12. 已知函数
则f(x)的反函数是______________
13. 巳知f( x ) = 3ax – 2a + 1，在区间[
-1，1 ]上存在
。使f( x0 ) = 0，则实数a的取值范围是_______________________。
14．若
且
，则
的取值范围是 ．
15．设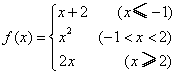
，若
，则
_____________。
16. 已知函数
的定义域是
，则m的取值范围是_______。
三 解答题(共6小题共76分，需写出解答或证明过程，否则不给分)
17．（12分）不等式
与
的解集分别为A，B，
试确定a，b的值，使A∩
，并求出A∪B．
18.(12分)
已知数列{an}满,, 其中a是非零常
数，设
1)求证：数列
是等差数列；
2)求数列
的通项公式.
19.
(12分) 已知函数
1)若函数的定义域是R求m的取值范围？
2)若函数的值域是R求m的取值范围？
20. (13分)已知函数
,当
时，
求f(x)的最小值g(a).
21．(13分) 季节性服装当季节即将来临时，价格呈上升趋势，设某服装开始时定价为10元，并且每周(7天)涨价2元，5周后开始保持20元的价格平稳销售；10周后当季节即将过去时，平均每周削价2元，直到16周末，该服装已不再销售.
1）试建立价格P与周次t之间的函数关系式.
2）若此服装每件进价Q与周次t之间的关系为Q＝－0.125(t－8)2＋12， t∈[5，10]，t∈N*，试问该服装第几周每件销售利润L最大?
22. (14分)已知二次函数f(x)=ax2+bx (a，b为常数，且a≠0)，满足f(1+x)=f(1-x),且方程f(x)=x有等根.
1)求f(x)的解析式；
2)是否存在实数m，n(m<n)，使f(x)的定义域和值域分别为[m，n]和[3m，3n]，若存在，求出m，n的值；若不存在，说明理由.
参考答案
一 选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | B | B | C | A | C | B | C | B | C |
二 填空题
11，117；12，
13，
或
；14，
或
；
15，
； 16，
；
三 解答题
17 设
，由A∩
得
，所以
或
，
或
18 (1)
，
，
，所以是首项为1/a
公差为1/a的等差数列.
(2)由
，
19 (1) 由题意得
(2) 由题意得
20 因
(1)当1<2a+1即a>0时，f(x)在[0,1]上递减，所以g(a)=f(1)=
(2)当2a+1<0即
时，f(x)在[0,1]上递增，所以g(a)=f(0)=a2
(3)当
时，f(x)的对称轴在[0,1]之间，所以g(a)=-3a2-4a-1.
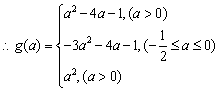
21.解析：
(1)P＝
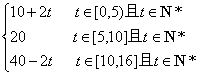
(2)因每件销售利润＝售价－进价，即L＝P－Q
t∈[5，10]时t∈N*时，L＝0.125t2－2t＋16
即t＝5时，Lmax＝9.125
由以上得，该服装第5周每件销售利润L最大.
22 (1)因方程f(x)=x有等根，即
有等根，所以b=1,
又f(1+x)=f(1-x)，则f(x)关于直线x=1对称，即
(2)
，
所以f(x)在[m，n]上递增，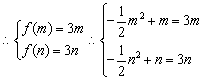
，又m<n
所以存在m=-4，n=0使f(x)定义域为[m，n]，值域为[3m，3n].