高一数学周练（十二） 参考答案
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | B | D | C | C | A | B | D | C | B | A | B |
13．
或
14．1 15．
，
16．
17．解：设其高为
，则由
可得：
解得
。
则圆台母线长为
，
圆台的全面积是
。
答：造这样的油桶约需
多少平方米材料
18．解：（Ⅰ）BC的中点是
，
过两点A，M的直线方程是：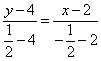
，
即
。
（Ⅱ）
直线BC的方程是
，即
，
点A到它的距离是
所以，△ABC的面积是
。
19．体积：
．
表面积：
。
20．解：（Ⅰ）直线
过定点
，而点又在圆内，
∴ 对
，直线
与圆C总有两个不同交点。
（Ⅱ）设圆心到直线的距离为
，
则
，又
，可得：
，
∴ 直线为
。
21．证明：（Ⅰ）由已知，△ABC与△BCD是直角三角形，
又平面ABC⊥平面BCD，平面ABC
平面BCD=BC，且CD⊥BC，
∴ CD⊥平面ABC，
又AC
平面ABC，AB平面ABC，
∴ CD⊥AC，CD⊥AB，
△ACD是直角三角形。
又 AB⊥AC，ACCD=C，
∴ AB⊥平面ACD，
AD平面ADC
∴ AB⊥AD，
△ ABD也是直角三角形。
所以，三棱锥A-BCD的四个面都是直角三角形
（Ⅱ）取AC中点M，过M作MN⊥BD，垂足为N，连MN。
∵ AB=AC，
∴ AM⊥BC，
又平面ABC⊥平面BCD，平面ABC平面BCD=BC，
∴ AM⊥平面BCD。
∵ BD平面BCD，
∴ AM⊥BD，
又MN⊥BD，MNBD=N，
∴ BD⊥平面AMN，
∴ BD⊥AN，即∠AMN是二面角A-BD-C的平面角。
设BC=
，则AM=
，BM=，
在Rt△BMN中，∠MBN=30°，
∴ MN=
，
△AMN中，
即二面角A-BD-C的正切值是2。
22．解：（1）设
，则
，
，显然直线
的斜率存在为：
，
∴ 直线：
，
即
。
（2）由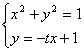
得：
，
解得或
，
∴ 
，
。
（3）
，
，
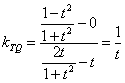即直线TP与TQ的斜率互为相反数，它们的倾斜角互补，即有由点P发出的光线，经AB反射后，反射光线通过点Q.