成都石室中学高2008级2005～2006学年度下期期中考试
数 学
第一卷（共76分）
一、选择题：每题只有唯一正确答案，每小题5分，共60分
1、以下各式能成立的是( )
A．
B．
且
C．
且
D．
2、已知
为第二象限角
终边上一点，且满足
，则
的值为( )
A．－ B．± C．－ D．
3、函数
，
是（ ）
A．增函数 B．减函数 C．奇函数 D．偶函数
4、已知
，则
的值为（
）
A．
B．
C．
D．
5、把函数
的图象向右平移
个单位,正好得到函数
的图象，则的最小正值是（ ）
A．
B．
C．
D．
6、正切型函数
图象的一个对称中心是（
）
A．
B．
C．
D．
7、函数
的值域为（
）
Ａ．
Ｂ．
Ｃ．
Ｄ．
8、若
，且
，则
的值应为（ ）
A．
B．
C．
D．
9、在
中，如果
，那么这个三角形的形状是( )
Ａ．锐角三角形 Ｂ．直角三角形 Ｃ．等腰三角形 Ｄ．等边三角形
10、函数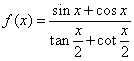
的最小正周期为（ ）
A．
B．
C．
D．
11、已知
，
，则
等于（ ）
A．
B．
C．
D．
12、设
,
,
，则( )
A.
B.
C.
D.
、
、
互不相等
二、填空题：每小题4分，共16分
13、若三个负数
，
，
依次成等比数列，则角
.
14、已知
是第四象限角，则化简
______ _____.
15、已知函数
满足
，则
.
16、如果函数
在区间
上是凸函数，那么对于区间内的任意
，
，…，
，都有
.若
在区间
上是凸函数，那么在
中，
的最大值是________________.
第二卷（共74分）
二、填空题：
13、____________________________. 14、____________. 15、____________. 16、____________.
三、解答题：共74分
17、（本小题满分12分）求值：
18、（本小题满分12分）已知函数
．
（1）求函数的定义域； （2）写出函数的最小正周期；
（3）求函数的值域； （3）求函数的单调递减区间．
19. （本小题满分12分）已知函数
（1）求函数的振幅，频率，初相；
（2）若存在常数
，使得函数
，
的值域为
，试求出的值．
20、（本小题满分12分）已知关于的方程
的两根为
和
，
．求：
(1) 
的值； (2) 方程的两根及此时
的值；
(3) 
＋
的值．
21、（本小题满分12分）己知函数
在
内取得一个最大值和一个最小值，且当
时，有最大值
，当
时，有最小值
．
（1）求函数
的解析式；
（2）是否存在实数，满足
？若存在，求出实数的取值范围；若不存在，说明理由
22、（本小题满分14分）
（1）求证：
（2）设集合
，
，
，求：
①实数的取值范围；
②
的值.
高2008级数学期中考试
参考答案
一、选择题：
ＣＡＤＤＣ ＡＢＡＣＢ ＣＡ
二、填空题：
１３、
和
； １４、； １５、
； １６、
．
三、解答题：
１７、解：原式=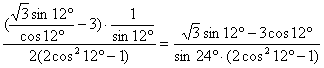
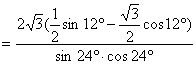
１８、解：（１）由
，
（２）
，
（３）
， 
，
（４）单调递减区间为：
，．
１９、解：
振幅为
，频率为
，初相是
（2）
，
，故
当
时，有
，且
解得 
当
时，同理可解得 
；
综上，或
２０、解：由题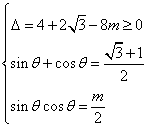
(１)
，
，所以
．
(２)∵sinθ＋cosθ＝． ∴ sinθ－cosθ＝．
∴方程两根分别为，． ∴θ＝或．
（3）原式=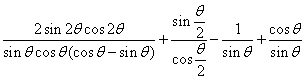
=
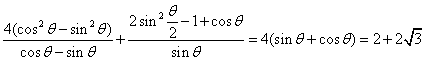
２１、解：(1)∵A＝3 
＝5π
T＝10π
∴ω＝
＝
π+φ＝
φ＝
∴y＝3sin(x+)
(2)∵ω
+φ＝
+ ∈(0, )
ω
+φ＝
+ ∈(0, )
而y＝sint在(0，)上是增函数
∴ω+φ＞ω+φ＞
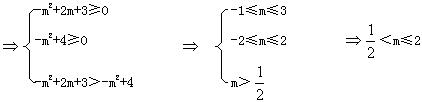
22、（1）证明：
（2）由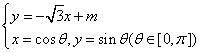
①
，
，
② 
，由已知，必有
，
故