ξ10向量的数量积.平移
编者：敬宗甫 杜厚君
一．知识精讲
1． 数量积的概念
（1） 向量的夹角：如图，已知两个向量a和b，使
=a,
b。则
叫做响亮a与b的夹角，记为<a,b>
（2） 数量积的定义：已知两向量a,b的夹角为
，则数量
叫做
a与b的数量积，记为
（3）数量积的集合意义：数量积
等于
的模与
在方向上的投影
的乘积
2．
数量积的性质：设
是单位向量。<
(1)
(2)a与b同向时，
；a与b反向的时候
。
（3）
或
（4）
（5）
3．运算律：（1）
(交换律) （2）
(与实数的集合律)
（3）
（乘法对加法的分配律）
没有结合律，可见向量的数量积完全遵循多项式运算法则
4． 向量数量积的坐标运算。
设
，则：
（1）
（2）
（3）
（4）
5．
两点间的距离公式：设A
，则
平移公式描述的是平移前的点与平移后的对应点坐标与平移向量的坐标之间的关系。
平移前的点
平移后的对应点
，平移向量的坐标
则 
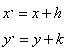
二．基础知识
1.若
，则在方向的投影为 （ ）
A 
B 
C 
D 
2．已知
，且
，则与的夹角为 （ ）
Ａ 
Ｂ 
Ｃ 
Ｄ 
3.设
是任意的非零平面向量，互相不共线，则下列命题中是真命题的有（ ）
① 
② 
③ 
不与
垂直 ④ 
Ａ ①② Ｂ ②③ Ｃ ③④ Ｄ ②④
4．已知点A
若向量
与
同向，
，则点B的坐标为（ ）
5．已知
，
，若向量与的夹角为钝角，则
的取值范围是 （ ）
Ａ 
Ｂ
Ｃ 
Ｄ 
6．
已知：函数
按向量平移所的图形解析式为
当
奇函数时，向量可以等于：
A 
B 
C （
）
D 
三．典型例题分析：
例1：已知
，当
为何值时，（1）
（2）
，平行时是同向还是反向？
变式1：已知：平面向量
，且
，
，求
以及与的夹角
例2：
，求
变式2：已知
都是非零向量，且
，求与
的夹角
例3：已知
且存在实数k和t，使
且
，试求
的最小值
例4．设函数
，（1）试根据函数
的图象，并写出变化过程
（2）
的图象是中心对称图形吗？（3）指出的单调区间
变式：将函数
的图象按向量平移后得到函数
的图形，求和实数
例5．将函数
的图象，按向量平移后得到的图象关于原点对称
，这样的向量是否唯一？若唯一，求出向量；若不唯一，求出最简向量
四．规律总结：
1． 平面向量的数量积及集合意义是本节的重点，用数量积处理向量垂直问题，向量长度，夹角是难点
2． 向量的数量积是两个向量之间的一种乘法运算，它是向量与向量的运算，结果是一个数量，所以向量的数量积的坐标表示是纯数量的坐标运算。
3．
向量与的夹角（1）当与平移成有公共起点时，两向量所成的角才是夹角
（2）
（3）cos<
=
4.配方法：待定系数法，代入法是确定平移向量的重要方法
五：闯关训练
1．若平面向量与向量=（1，-2）的夹角是
，且
，则
（ ）
A （-3，6） B （3，-6） C （6，-3） D（-6，3）
2．若向量垂直与向量和，
且
，则 （ ）
A 
B 
C 不平行与，也不垂直与 D 以上情况都有可能
3．已知，均为单位向量，它们的夹角为，那么
（ ）
A 
B 
C 
D 4
4． 给出下列命题：
① 若
则
②
已知 是三个非零向量，若
则
③
在三角形ABC中，a=5,b=8,c=7，则
④
与是共线向量
其中正确的命题序号是
5．
已知
与的夹角为
，求当向量
与
的夹角为锐角时，的取值范围。
6．如图：以原点O和A
为两个顶点作等腰直角三角形OAB使
求点B的坐标和向量
的坐标。
7．已知：平面向量
，
求证：
（2） 若存在不同时为零的实数k和t ，使
且，试确定函数关系
（3）
根据（2）的结论确定函数的单调区间
8．已知：
的图象F按
平移得到
，已知A（0，8）
在上，F与的交点是B（
，试求F对应的函数解析式。