直线的方程
班级 学号______________ 姓名
一、选择题(每小题5分,共40分):
1、若直线![]() 的倾斜角为
的倾斜角为![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.不存在
D.不存在
2、经过两点![]() 的直线的倾斜角为
的直线的倾斜角为![]() ,则
,则![]() 的值等于(
)
的值等于(
)
A ![]() B
B
![]() C 0 D 2
C 0 D 2
3、过点(![]() ,4)作直线
,4)作直线![]() 使点M(1,2)到直线
使点M(1,2)到直线![]() 距离最大,则直线
距离最大,则直线![]() 的方程为( )
的方程为( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
4、如果![]() 且
且![]() ,那么直线
,那么直线![]() 不通过(
)
不通过(
)
A 第一象限 B 第二象限 C 第三象限 D 第四象限
5、经过点A(1,2),且在两坐标轴上的截距相等的直线共有( )
A 1条 B 2条 C 3条 D 4条
6、已知直线![]() 的倾斜角为
的倾斜角为![]() ,则
,则![]() 的值是(
)
的值是(
)
A ![]() 或4 B
或4 B ![]() 或2
C 4或0
D 0或
或2
C 4或0
D 0或![]()
7、直线![]() 与直线
与直线![]() 关于点
关于点![]() 对称,则直线
对称,则直线![]() 的方程是(
)
的方程是(
)
A ![]() B
B ![]() C
C ![]() D
D ![]()
8、直线![]() 与
与![]() 平行,则实数
平行,则实数![]() 的值为( )
的值为( )
A . 1 B.-1或1 C .-1 D. 0
选择题答案栏
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 |
二、填空题(每小题5分,共20分):
9、过点(1,![]() ),倾斜角是直线
),倾斜角是直线![]() 的倾斜角的2倍的直线方程是 。
的倾斜角的2倍的直线方程是 。
10、无论a取何实数,直线(1+2a)x+(3a-2)y+9a+1=0(a![]() )必经过定点,这个定点的坐标是______________。
)必经过定点,这个定点的坐标是______________。
11、已知点N(3,1),点A、B 分别在直线![]() 和
和![]() 上,则
上,则![]() 的周长的最小值是
。
的周长的最小值是
。
12、设三条直线![]() 和
和![]() 围成直角三角行,则
围成直角三角行,则![]() 的值是
。
的值是
。
三、解答题:
13(8分). 求直线![]() 关于直线
关于直线![]() 对称的直线的方程。
对称的直线的方程。
14(10分).已知直线![]() 过两条直线
过两条直线![]() 的交点,且与
的交点,且与
A(2,3),B(-4,5)两点的距离相等,求直线![]() 的方程。
的方程。
15(10分).过点P(0,1)作直线![]() ,使它被两已知直线
,使它被两已知直线![]()
![]() 所截得的线段平分与点P,求直线
所截得的线段平分与点P,求直线![]() 的方程。
的方程。
16(12分).直线![]() 是
是![]() 中
中![]() 的平分线所在直线,若A、B的坐标分别为A(-4,2),B(3,1),求点C的坐标,并判断
的平分线所在直线,若A、B的坐标分别为A(-4,2),B(3,1),求点C的坐标,并判断![]() 的形状。
的形状。
直线的方程(参考答案)
一、选择题答案(每小题5分,共40分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 | C | B | D | C | B | A | D | C |
二、填空题(每小题5分,共20分):
9、![]() ;
10、(-3,-1);
;
10、(-3,-1);
11、![]() ;
12、0,
;
12、0,![]() .
.
三、解答题:
13(8分). 求直线![]() 关于直线
关于直线![]() 对称的直线的方程。
对称的直线的方程。
解:在直线![]() 上取两点A(-1,0)和B(0,3)
上取两点A(-1,0)和B(0,3)
则A(-1,0)和B(0,3)关于直线![]() 的对称点分别为
的对称点分别为
![]() (2,-3)和
(2,-3)和![]() (5,-2)
(5,-2)
由两点式得所求直线为![]() .
.
14(10分).已知直线![]() 过两条直线
过两条直线![]() 的交点,且与
的交点,且与
A(2,3),B(-4,5)两点的距离相等,求直线![]() 的方程。
的方程。
解:直线![]() 的交点为(-1,2),
的交点为(-1,2),
若直线![]() 平行直线AB,易求得直线
平行直线AB,易求得直线![]() 的方程为
的方程为![]() ;
;
若直线![]() 通过线段AB的中点,易求得直线
通过线段AB的中点,易求得直线![]() 的方程为
的方程为![]()
所以直线![]() 的方程为
的方程为![]() .
.
15(10分).过点P(0,1)作直线![]() ,使它被两已知直线
,使它被两已知直线![]()
![]() 所截得的线段平分与点P,求直线
所截得的线段平分与点P,求直线![]() 的方程。
的方程。
解:设![]() 分别与
分别与![]() 、
、![]() 分别交于A、B.设B(t,8-2t),由中点坐标公式可得
A(-t,2t-6),又A在
分别交于A、B.设B(t,8-2t),由中点坐标公式可得
A(-t,2t-6),又A在![]() 上,故(-t)-3(2t-6)+10=0,解得t=4.
上,故(-t)-3(2t-6)+10=0,解得t=4.
所以A(-4,2) B(4,0)
由两点式得![]() 的方程为x+4y-4=0.
的方程为x+4y-4=0.
16(12分).直线![]() 是
是![]() 中
中![]() 的平分线所在直线,若A、B的坐标分别为A(-4,2),B(3,1),求点C的坐标,并判断
的平分线所在直线,若A、B的坐标分别为A(-4,2),B(3,1),求点C的坐标,并判断![]() 的形状。
的形状。
解:由平几知识得点A关于直线![]() 的对称点
的对称点![]() 必在直线BC上。
必在直线BC上。
设![]() (a,b)则有
(a,b)则有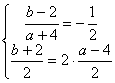
![]() 故
故![]() 的坐标为(4,-2)
的坐标为(4,-2)
由两点式得直线BC的方程为![]()
解方程组![]() 点C的坐标为(2,4).
点C的坐标为(2,4).
又![]() ,得
,得
![]() 为直角三角形
为直角三角形