萧山二职2005学年第一学期第一次质量检测卷
高三职高 数学学科 三（4，5，6，10） 命卷人：陈国伟
一．选择题（3*10）
1． 下列书写正确的是 （ ）
A．
B。
C。
D。
2．已知
，则
是
的
（ ）
A．充分非必要条件 B。必要非充分条件
C．充要条件
D。既非充分又非必要条件
3．不等式
的解集是
（ ）
A．
B。
C。
D。
4．不等式
的解集是
（ ）
A．
B。
C。
D。
5．若奇函数在
上是减函数，则
与
的大小关系为 （ ）
A．
B。
C．
D。不能确定
6．函数
与
（其中
）的图像只可能是 （ ）
 |  |
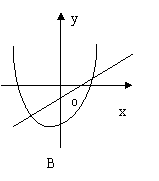
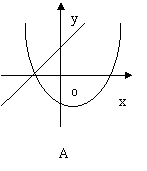
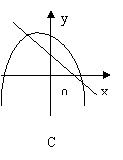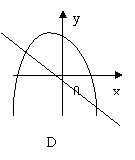7.下列解析式中，定义域为全体实数的是 （ ）
A．
B。
C．
D。
8．
的大小关系
（
）
A．
B。
C．
D。
9．已知
，则
=
（
）
A．
B。
C．
D。
10．函数
是
（
）
A．奇函数 B。偶函数
C．既不是奇函数又不是偶函数 D。既是奇函数又是偶函数
二．填空题（4*10）
11．设
，则
。
12．当
时，
，当
时，等号成立。
13．若直角坐标内的点
在第四象限，则
的取值范围为____________。
14．已知
的解集是
，则
的解集是___
________________。
15．函数
的单调减区间是________________。
16．函数
的值域是__________________。
17．函数
的定义域为____________________。
18．
。
19．已知
，用
表示
。
20．函数
在区间____________上是增函数。
三．计算，证明题
21．设
，若
，求
（5 分）
22．实数
取何值时，关于
的方程
的两根的平方和最小？
并求出最小值。（5分）
23．已知
，集合
，
求（1）
的表达式
（2）当
时，求的最小值和最大值。（7分）
24．已知二次函数
的解集是
，求函数
的解析式。（5分）
25．已知函数
的图象过原点，（1）若
成等差数列，求的值；（2）若
，三个正数
成等比数列，求
证：
。（8分）