实数和向量的积
【基础知识精讲】
1.实数与向量的积的定义
实数λ与向量
的积是一个向量，记λ，它的长度与方向规定如下：
(1)｜λ｜=｜λ｜·｜｜;
(2)当λ＞0时，λ的方向与的方向相同；当λ＜0时，λ的方向与的方向相反；当λ=0时，λ=
,方向是任意的.
2.实数和向量的积的运算律
设λ、μ为实数，那么：(1)λ(μa)=λμ
(2)(λ+μ) =λ+μ
(3)λ(+
)=λ+λ
3.两个向量共线定理
向量与非零向量共线的充要条件是有且只有一个实数λ，使得=λ.
4.平面向量基本定理
如果
，
，是同一平面内的两个不共线向量，那么对这一平面内的任一向量，有且只有一对实数λ1，λ2使：
=λ1+λ2
其中不共线的向量，叫做表示这一平面内所有向量的一组基底.
注意：(1)平面内的任一向量都可以沿两个不共线的方向分解成两个向量和的形式.
(2)上面分解是唯一的.
向量的加法、减法、实数与向量的积的混合运算称为向量的线性运算，也叫做向量的初步运算.任一平面直线型图形都可以表示为某些向量的线性组合.
【重点难点解析】
1.实数与向量的积的运算律与实数乘法的运算律很相似，只是实数与向量相乘的分配律有两种不同形式.
(λ+μ) =λ+μ和λ(+)=λ+λ；实数与向量相乘的运算中的关键是等式两边向量的模相等的同时，方向也必须相同.
2.掌握实数与向量积的概念，运算及两个向量共线的充要条件.
例1
化简
［(4-3)+
-
(6-7)］= .
例2
设，是不共线的两个向量，已知
=2+k，
=+, 
=-2，若A、B、D三点共线，求k的值.
例4
已知□ABCD，E、F分别是DC和AB的中点，判断
、
是否平行?
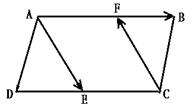
分析：要判断、是否平行，就是判断能否用表示出来.
解：设=,
=因为E、F分别是DC和AB的中点
所以
=
= =
例5
求向量
,
:
【难题巧解点拔】
例1
设M为△ABC的重心，证明对任意一点O，有
=( 
+
+
)
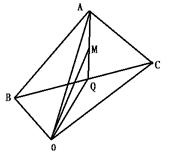
例2
如图，已知在△ABC中，D是BC上的一点，且
=λ.
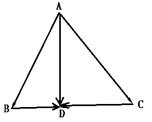
试证：=
例3
若O、A、B三点不共线，已知
=m·+n·,m·n∈R,且m+n=1,那么P点位置如何?请说明理由.
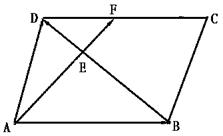
例4 求证：平行四边形一顶点和对边中点的连线三等分此平行四边形的一条对角线(如图)
【典型热点考题】
例1
若=3, =-5且｜｜=｜｜,则四边形ABCD是( )
A.平行四边形 B.菱形 C.等腰梯形 D.非等腰的梯形
例2 已知λ，u∈R，则在以下各命题中，正确的命题共有( )
(1)λ＜0，≠时，λ与的方向一定相反
(2)λ＞0，≠时，λ与的方向一定相同
(3)λ≠0，≠时，λ与是共线向量
(4)λu＞0，≠时，λ与u的方向一定相同
(5)λu＜0，≠时，λ与u的方向一定相反
A.2个 B.3个 C.4个 D.5个
例3
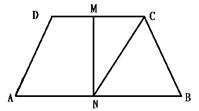
梯形ABCD，AB∥CD，且
，M、N分别是DC和AB的中点，如图，若=,=，试用，表示和
，则=
.
