2003-2004学年度下学期
高中学生学科素质训练
高一数学同步测试(3)—正、余弦的诱导公式
一、选择题(每小题5分,共60分,请将所选答案填在括号内)
1.若![]() 那么
那么![]() 的值为 ( )
的值为 ( )
A.0 B.1 C.-1 D.![]()
2.已知![]() 那么
那么![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.已知函数![]() ,满足
,满足![]() 则
则![]() 的值为 ( )
的值为 ( )
A.5 B.-5 C.6 D.-6
4.设角![]()
![]() 的值等于 ( )
的值等于 ( )
A.![]() B.-
B.-![]() C.
C.![]() D.-
D.-![]()
5.在△ABC中,若![]() ,则△ABC必是 ( )
,则△ABC必是 ( )
A.等腰三角形 B.直角三角形
C.等腰或直角三角形 D.等腰直角三角形
6.当![]() 时,
时,![]() 的值为 ( )
的值为 ( )
A.-1 B.1 C.±1 D.与![]() 取值有关
取值有关
7.设![]() 为常数),且
为常数),且![]()
那么![]() ( )
( )
A.1 B.3 C.5 D.7
8.如果![]() 则
则![]() 的取值范围是 ( )
的取值范围是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
9.在△ABC中,下列各表达式中为常数的是 ( )
A.![]() B.
B. ![]()
C.![]() D.
D.![]()
10.下列不等式上正确的是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
11.设![]() 那么
那么![]() 的值为 ( )
的值为 ( )
A.![]() B.-
B.-![]() C.
C.![]() D.
D.![]()
12.若![]() ,则
,则![]() 的取值集合为 ( )
的取值集合为 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
二、填空题(每小题4分,共16分,请将答案填在横线上)
13.已知![]() 则
则![]() .
.
14.已知![]() 则
则![]() .
.
15.若![]() 则
则![]() .
.
16.设![]() ,其中m、n、
,其中m、n、![]() 、
、![]() 都是非零实数,若
都是非零实数,若
![]() 则
则![]() .
.
三、解答题(本大题共74分,17—21题每题12分,22题14分)
17.设![]() 和
和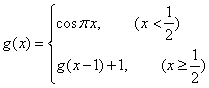
求![]() 的值.
的值.
18.已知![]() 求证:
求证:![]()
19.已知![]() 、
、![]() 是关于
是关于![]() 的方程
的方程![]() 的两实根,且
的两实根,且![]()
求![]() 的值.
的值.
20.已知![]()
(1)求![]() 的表达式;
的表达式;
(2)求![]() 的值.
的值.
21.设![]() 满足
满足![]() ,
,
(1) 求![]() 的表达式;
的表达式;
(2) 求![]() 的最大值.
的最大值.
22.已知数列![]() 的通项公式为
的通项公式为![]() 记
记![]()
求![]()
高一数学参考答案(三)
一、1.C 2.B 3.B 4.C 5.C 6.A 7.C 8.C 9.C 10.B 11.B 12.C
二、13.![]() 14.0 15.1 16.-1
14.0 15.1 16.-1
三、17.![]() ,
, ![]()
![]() , 故原式=3.
, 故原式=3.
18.由已知![]() ,
,
![]() .
.
19.由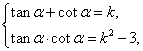 知原式=
知原式=![]() .
.
20.(1)![]() ,
,
![]() .
.
(2)![]() .
.
21.(1)由已知等式
![]() ①
①
得 ![]() ②
②
由3![]() ①-②,得
①-②,得
8![]() ,
,
故![]() .
.
(2)对![]() ,将函数
,将函数![]() 的解析式变形,得
的解析式变形,得
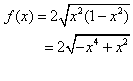
=![]() ,
,
当![]() 时,
时,![]()
22.![]()
=![]()
=![]()
审定意见:本套试题题型比较全面,对第21题增加了一小问,增添了题中的一些标点符号。
审稿人:安振平