高一期末检测题
一、选择
1.设集合![]() 则 ( )
则 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
2.已知a,b,c成等比数列,且x,y分别为a与b、b与c的等差中项,则![]() 的值为( )
的值为( )
(A)![]() (B)-2 (C)2 (D) 不确定
(B)-2 (C)2 (D) 不确定
3.函数y=![]() 的定义域是( )
的定义域是( )
(A)-2![]() (B)-2
(B)-2![]()
(C)x>2
(D)x![]()
4在数列![]() ,则该数列中相邻两项的乘积是负数的
,则该数列中相邻两项的乘积是负数的
是 ( )
A.![]() B.a22·a23 C.a23·a24 D.a24·a25
B.a22·a23 C.a23·a24 D.a24·a25
5.![]() 2的必要非充分条件是 ( )
2的必要非充分条件是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6. 函数f(x)=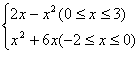 的值域是( )
的值域是( )
(A)R (B)[-9,+![]() ) (C)[-8,1] (D)[-9,1]
) (C)[-8,1] (D)[-9,1]
7.函数y=logax当x>2 时恒有![]() >1,则a的取值范围是( )
>1,则a的取值范围是( )
(A)![]() (B)0
(B)0![]()
(C)![]() (D)
(D)![]()
8.函数y=x2-3x(x<1)的反函数是( )
(A)y=![]() (x>-
(x>-![]() )
(B)y=
)
(B)y=![]() (x>-
(x>-![]() )
)
(C)y=![]() (x>-2)
(D)y=
(x>-2)
(D)y=![]() (x>-2)
(x>-2)
9.函数f(x)的图像与函数g(x)=(![]() )x的图像关于直线y=x对称,则f(2x-x2)的单调减区间为( )
)x的图像关于直线y=x对称,则f(2x-x2)的单调减区间为( )
(A)(0,1) (B)[1,+![]() ) (C)(-
) (C)(-![]() ,1] (D)[1,2)
,1] (D)[1,2)
10.下列命题中是真命题的是( )
(A)数列{an}是等差数列的充要条件是an=pn+q(p![]() )
)
(B)已知一个数列{an}的前n项和为Sn=an2+bn+a,如果此数列是等差数列,那么此数列也是等比数列
(C)数列{an}是等比数列的充要条件an=abn-1
(D)如果一个数列{an}的前n项和Sn=abn+c(a![]() 0,b
0,b![]() 0,b
0,b![]() 1),则此数列是等比数列的充要条件是a+c=0
1),则此数列是等比数列的充要条件是a+c=0
11.由于电子技术的飞速发展,计算机的成本不断降低,若每隔5年计算机的价格降低![]() ,现在价格8100元的计算机15年后的价格为( )
,现在价格8100元的计算机15年后的价格为( )
(A)300元 (B)900元 (C)2400元 (D)3600元
12.已知定义在R上的函数y=f(x)满足下列三个条件:①对任意的x∈R都有![]() ②对于任意的
②对于任意的![]() ,都有
,都有![]() ③
③![]() 的图象关于y轴对称,则下列结论中,正确的是 ( )
的图象关于y轴对称,则下列结论中,正确的是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
二、填空题(每小题4分,共16分)
13.若f(x)=![]() 在区间(-2,+
在区间(-2,+![]() )上是增函数,则a的取值范围是
)上是增函数,则a的取值范围是
14.在2和30之间插入两个正数,使前三个数成等比数列,后三个数成等差数列,则插入的这两个数的等比中项为
15.已知f(x)=log![]() x,则不等式[f(x)]2>f(x2)的解集为--------
x,则不等式[f(x)]2>f(x2)的解集为--------
16.已知整数对的序列如下:(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),(1,5),(2,4),……,则第60个数对为
三、解答题
17.已知数列{an}的通项公式为an=3n+2n+(2n-1),求前n项和。
18.若函数y=![]() 的定义域为R,求实数k的取值范围。
的定义域为R,求实数k的取值范围。
19.某人于1999年5月1日去银行存款a元,存的是一年定期储蓄,2000年5月1日他将到期存款的本息一起取出,再加入a元后,还存一年定期储蓄,此后每年5月1日他都按照同样的方法,在银行取款和存款,设银行一年定期储蓄的年利率r不变,则到2004年5月1日,他将所有的存款和利息全部取出时,取出的钱数共有多少
20.(本题满分12分)
某医药研究所开发一种新药,如果成人按规定的剂量服用,据监测:服药后每毫升血液中的含药量y与时间t之间近似满足如图所示的曲线.
(1)写出服药后y与t之间的函数关系式;
(2)据测定:每毫升血液中含药量不少于4微克时治疗疾病有效,假若某病人一天中第一次服药时间为上午7:00,问一天中怎样安排服药的时间(共4次)效果最佳?
|
21.已知a>0,函数![]()
(1)当b>0时,若对任意![]() ;
;
(2)当b>1时,证明:对任意![]() 的充要条件是
的充要条件是![]()