高一三角单元小结1
一、基本概念、定义、公式：
1、角是一条射线饶着它的端点旋转形成的几何图形，它由 、 、 组成。
2、角的概念推广后，包括 、 、 ，
与α终边相同的角表示为 。
角的集合：终边在x轴上 在y轴上
在第一象限 在第二象限
在第二四象限 在直线y＝x上
3、弧度制：把 叫1弧度的角。
公式：α＝
换算：180°＝ 弧度；
1弧度＝ 度； 1°＝ 弧度
扇形： 弧长L＝ ，面积S＝
＝ =
4、 任意角的三角函数：
① 定义：在角α终边上任取一点P(x，y)，它与原点的距离r＝ （r
0），六个三角函数的定义依次是
、
、
、
、 、 。
②三角函数的定义域：
、
的定义域为 ；
、
的定义域为
；
、
的定义域为
。
③三角函数值的符号：当
在
象限时，
；当在 象限时，
；当在
象限时，
。
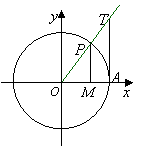④三角函数线：
如图，角的终边与单位圆交于点P，过点P作 轴的垂线，
垂足为M，则
。过点A(1,0)作 ，
交 于点T，则 。
⑤同角三角函数关系式：
平方关系：
商数关系：
倒数关系：
⑥诱导公式：
| ―α(或2π―α) | π+α | π－α | 2kπ+α | |
| sin | ||||
| cos | ||||
| tan |
二、 习题训练
（一）选择题
1、若角α满足sinαcosα<0,cosα-sinα<0,则α在 ( )
A．第一象限 B.第二象限
C．第三象限 D．第四象限
２、如果1弧度的圆心角所对的弦长为2，则这个圆心角所对的弧长为 ( )
A． B．sin0.5 C．2sin0.5 D．tan0.5
３、已知圆中一段弧长正好等于该圆的外切正三角形的边长，那么这段弧所对的圆心角的弧度数为 ( )
A． B． C． D．2
４、(04浙江)在△ABC中，“A＞30°”是“sinA＞”的 ( )
A．仅充分条件 B．仅必要条件 C．充要条件 D．既不充分也不必要条件
５、已知sinα＞sinβ，则下列命题成立的是 ( )
A．若α.β是第一象限角，则cosα＞cosβ．
B．若α.β是第二象限角，则tanα＞tanβ．
C．若α.β是第三象限角，则cosα＞cosβ．
D．若α.β是第四象限角，则tanα＞tanβ．
６、以下各式能成立的是 ( )
A．sinα＝cosα＝ ； B．cosα＝且tanα＝2；
C．sinα＝且tanα＝； D．tanα＝2且cotα＝－
７、的结果是 ( )
A．1 B．0 C．－1 D．
８、设sin123°＝a，则tan123°＝ ( )
A． B． C． D．
９、α为第二象限角，P(x, )为其终边上一点，且cosα＝x，则x值为 ( )
A． B．± C．－ D．－
10、若α满足＝2，则sinα·cosα的值等于 ( )
A． B．－ C．± D．以上都不对
（二）填空题：
11、已知sinθ－cosθ＝，则sin3θ－cos3θ＝ ．
12、函数y＝＋＋＋的值域为 ．
13、已知cos(75°＋α)＝，其中α为第三象限角，则cos(105°－α)＋
sin(α－105°)＝ ．
14、若θ满足cosθ>
,则角θ的取值集合是
．
（三）解答题：
15、已知扇形的周长为L，问当扇形的圆心角α和半径R各取何值时，扇形面积最大？
16、已知
，
，若
是第二象限角，求实数
的值.
17、已知α为第三象限角，且f(α)＝．
(1)化简f(α)； (2)若cos(α－)＝，求f(α)的值； (3)若α＝－1860°，求f(α)的值．
18、已知关于x的方程2x2－(＋1)x＋m＝0的两根为sinθ和cosθ，θ∈(0,2π)，求：
(1) ＋的值； (2)m的值； (3)方程的两根及此时θ的值．
参考答案：
一、基本概念、定义、公式：略
二、习题训练
（一）选择题：BADB DCAD CB
（二）填空题：
11． 12．{－2,0,4} 13、 14、
提示：13、α为第三象限角，cos(75°＋α)＝ ，∴sin(75°＋α)＝－，
cos(105°－α)＝―cos[180°―(105°―α)]＝－cos(75°＋α)＝－，
sin(α－105°)＝－sin[180°＋(α－105°)]＝－sin(75°＋α)＝，∴原式＝．
（三）解答题：
15、解：∵L＝2R＋αR，S＝αR2．∴α＝．∴L＝2R＋
2R2－LR＋2S＝0．
△＝L2－16S≥0S≤．故当α＝2．R＝时，Smax＝．
16、解：依题意是第二象限角，
∴
，
，又
，从而得：
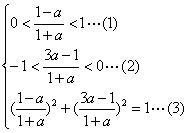
由（3）解得
或
，把代入不符合不等式（1）故舍去，从而
17．(1)f(α)＝－cosα． (2) f(α)＝． (3) f(α)＝－．
18、解：依题得：sinθ＋cosθ＝，sinθcosθ＝．
∴(1)原式＝＋＝sinθ＋cosθ＝；
(2)m＝2 sinθcosθ＝(sinθ＋cosθ)2－1＝．
(3)∵sinθ＋cosθ＝．∴ sinθ－cosθ＝．
∴方程两根分别为，．∴θ＝或．