《角的概念的推广与弧度制》
一、复习要求：
1． 理解正角、负角、零角这三个概念，关键是终边的旋转方向。
2． 象限角、区间角、终边相同的角和轴线角这几个概念的区别与联系。
3．
正确理解几个有特殊含义的角，如：“
到
的角”、“第一象限的角”、“锐角”和“小于的角”。
4． 角度制与弧度制的区别与联系（角度与弧度的相互转化）。
二、复习重点：
1． 识别、理解并能正确表示各种角，理解弧度制概念的建立及弧度与角度的换算。
2． 能按不同的要求写出符合条件的角的集合和有符号语言正确地表示它们。
三、复习过程：
1．知识及重要方法落列：
正角、负角、零角；象限角、区间角、终边相同的角和轴线角；角度与弧度的相互转化。
方法：例举法，特殊值法，分类讨论，几何法，数形结合。
2．典型例题分析：
例1．若时针走过2小时40分，则分针走过的角是多少？
解：2小时40分=
小时，
故分针走过的角为
。
练习1： 将钟表上的时针作为角的始边，分针作为角的终边，那么当钟表上显示8点5分时，时针与分针构成的最小正角是 （逆时针旋转为正，顺时针旋转为负）
例2．自行车大链轮有48个齿，小链轮有20个齿，当大链轮转过一周时，求小链转过的弧度数。
解：当大链轮转过一周，即转过48个齿时，小链轮也必须同步转过48个齿，故小链轮转过了
周。
所以，小链轮转过的弧度数为
。
练习2： 直径为10cm的 滑轮上有提条长为6cm的弦，P是此弦的中点，若滑轮以每秒5弧度的角速度旋转，则 经过5秒钟后，点P经过的弧长等于 。
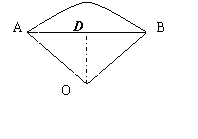
例3．弧度为2的圆心所对的弦长为2，则这个圆心角所对的弧长是多少？这个圆心角所夹的扇形的面积是多少？
解：如图，过O作 
于D。有垂径定理知D为AB的中点，
所以，扇形的半径 ：
有弧长公式 l=ar ，得
由扇形面积公式
，得
所以，弧长为 
，面积为
。
练习3： 若一圆弧的长等于其所在圆的内接正三角形的边长，那么其圆心角的弧度数是 。
点评：
上述例题主要考察弧度制的概念及应用，考察弧度制下的弧长公式和扇形面积公式及应用。考察平面几何知识在三角问题中的应用。要注意，在使用公式l=ar及
时，圆心角的单位必须是弧度。
3．小结：
4．作业：
（1）下列命题正确的是： （ ）
（A）终边相同的角一定相等。 （B）第一象限的角都是锐角。
（C）锐角都是第一象限的角。
（D）小于
的角都是锐角。
（2）若a是第一象限的角，则
是第
象限角。
（3）若
的终边关于y轴对称，则必有（ ）
（A）
（B）
（C）
（D）
（4）若
，且角a与
的角的终边垂直，求满足条件的a的集合。