泰顺一中02-03高一数学下学期期末复习综合练习（一）
苏志清 浙江省泰顺县第一中学
座号 姓名 得分___________
一、选择题（每题3分，共36分）
1 若半径为120mm的圆上，有一条弧的长是144mm，则此弧所对的圆心角的度数是（ ）
(A) 1.2 (B)1.3 (C)1.4 (D)12
2已知角
的正切线是单位长度的有向段线段，那么角的终边（ ）
(A)在
轴上
(B)在
轴上
(C)在直线
上
(D) 在直线上或
上
3已知
那么
的值是（ ）
(A)
(B)
(C)
(D)
4化简
(A)１ (B)－１ (C)０ (D)２
5计算
（ ）
(A)
(B)
(C)
(D)1
6.已知
那么
( )
(A)4
(B)
(C)
(D)2
7.函数
R （ ）
(A)是奇函数 (B) 是偶函数
(C)既不是是奇函数也不是偶函数 (D)有无奇偶性不能确定
8为了得到函数
R的图象，只需把函数
R的图象上所有的点的（ ）
(A)横坐标伸长到原来的两倍，纵坐标不变 (B) 横坐标缩到原来的
倍，纵坐标不变
(C) 纵坐标伸长到原来的两倍，横坐标不变 (D) 纵坐标缩到原来的倍，横坐标不变
9函数
的单调区间是（ ）
(A)
(B) 
(C) 
(D) 
10.以
、
、
为顶点的三角形是直角三角形的是（
）
(A) 
(B) 
(C)
(D)
11一个函数的图象按
平移后得到的图象的函数解析式为
，则原函数的解析式是（ ）
(A)
(B) 
(C)
(D)
12平形四边形两条邻边的长是
mm和
mm，它们的夹角是
，那么这个平形四边形的面积是（
）
(A)36
(B)76
(C)24
(D)48
二、填空题（每题4分，共24分）
13已知
且
与
的夹角
，则
.
14已知两点
、
，则点
分有向线段
所成的
= .
.
15已知点
及
则D的坐标 .
16已知
则
.
17飞机从甲地按北偏西
的方向飞行1400km到达乙地，再从乙地按南偏东
的方向飞行1400km到达丙地.那么丙地在甲地的方向是
.丙地距甲地_______________km..
18.已知
且
，则
三、解答题（本题共4题，满分40分）
19.（本题小题满分10分）已知
且
求
的值.
20. （本题小题满分12分）已知函数
R, 问:
⑴函数的最小正周期是什么?
⑵函数什么在区间上是增函数？
⑶函数的图象可以由函数
R的图象经过怎样的变换得出？
21. （本题小题满分8分）设
是非零向量，且
，求证：
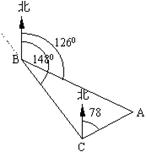
22. （本题小题满分12分）如图，货轮在海上以35 n mile/h的速度沿着方位角为
的方向航行.为了确定船位，在点观测灯塔的方位角是
，航行半小时后到达点，观测的灯塔的方位角是
.求货轮到达点时与灯塔的距离（精确到1 n mile）.
参考数据：
泰顺一中02-03高一数学（下）期末复习综合练习（一）
一、选择题（每小题3分，共36分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | D | D | C | C | D | A | B | C | D | B | D |
二、填空题（每小题4分，共24分）
13.
. 14.
. 15.
. 16.
17.,1400km.
18.
.
三、解答题（本题共4题，满分40分）
19（本题小题满分10分）
解：∵
∴
,
-1.
20（本题小题满分12分）
解：
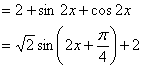
⑴ 
⑵由正弦函数的性质可知
∴ 
∴函数在
上是增函数.
⑶由已知函数可变为：
，R可知
函数的图像可以由函数R的图象向左平移
个单位，再向上平移2各单位得到.
21（本题小题满分8分）
证明： 
22（本题小题满分12分）
解：由已知得 
，
∴
由正弦定理得
∴
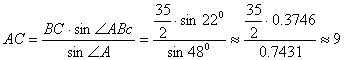
答：货轮到达点时与灯塔的距离是9 n mile.