2004-2005学年南阳第三实验高中第一学期
高一数学期末质检题
高一( )班 姓名 学号 得分
(全部答在答题卷上!!!!!)
一、 选择题:
1、设集合P={(x,y)│y=x2},集合Q={(x,y) │y=x}则P∩Q等于 ( )
A、{(0,0)} B、{(1,1)} C、{(0,0),(1,1)} D、{0,1}
2、在等差数列{an}中,已知a4+a6=18,a2=3,则a8= ( )
A、 9 B、 15 C、 17 D、 21
3、若数列![]() 的前n项之和
的前n项之和![]() ,那么这个数列的通项公式为( )
,那么这个数列的通项公式为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4、已知![]() ,则
,则![]() 的大小关系 ( )
的大小关系 ( )
A、![]() <
<![]() <
<![]() B、
B、![]() >
>![]() >
>![]() 、
、
C、![]() >
>![]() >
>![]() D、
D、![]() >
>![]() >
>![]()
5、等差数列![]() 的首项是
的首项是![]() 公差
公差![]() ≠0,如果
≠0,如果![]() 成等比数列,那么
成等比数列,那么![]() ( )
( )
A、3
B、2 C、![]() D、2或
D、2或![]()
6、.设命题甲:x-2<3:命题乙:0<x<5;那么甲是乙的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
7、设![]() ,则
,则![]() 的值为( )
的值为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
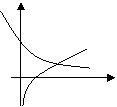
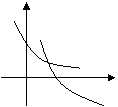
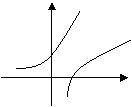
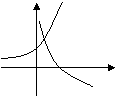
8、已知![]() ,
,![]() ,若
,若![]() , 则
, 则![]() 与
与![]() 同一坐标系内的图象可能是
( )
同一坐标系内的图象可能是
( )
 y
y
y
y
y
y
y
y
O x 0 x 0 X 0 X
A B C D
9、函数![]() 的反函数是
( )
的反函数是
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
10、设P={3,4,5},Q={4,5,6,7},定义![]() ,则P※Q中元素个数为
,则P※Q中元素个数为
A.3 B.4 C.7 D.12
11.数列1, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ……的前100项之和为 :
……的前100项之和为 :
A 10 B ![]() C 11 D
C 11 D ![]()
12.在数列{an}中,an≠0(n∈N*),且满足![]() 则数列
则数列![]() 是 ( )
是 ( )
A.递增的等差数列 B.递减的等差数列
C.递增的等比数列 D.递减的等比数列
二、填空题:
13、等比数列{an}中,S2=7,S6=91,则S4= .
14、函数f(x) = log ax(a>0,a≠1),若f(x1)-f(x2)
=1,则![]() 等于________.
等于________.
15、已知等差数列的前四项的和为124,后四项的和为156,又各项的和为210,则此等差数列共有 项。
16、已知![]() , 那么实数
, 那么实数![]() 的取值范围是
的取值范围是
三、解答题:
17、(本小题满分12分)
已知全集为R,集合A={x│x2-2x-3≤0},B={x│![]() <1}
<1}![]()
(Ⅰ)求CRA;(Ⅱ)求A∩(CRB).
18、(本小题满分12分)
已知数列{![]() }的前n项和为Sn.=2
}的前n项和为Sn.=2![]() -3.
-3.
(Ⅰ)求数列{![]() }的通项公式
}的通项公式![]() ;(Ⅱ)设
;(Ⅱ)设![]() =
=![]() ,,求数列{
,,求数列{![]() }前n项和。
}前n项和。
19、(本小题满分12分)
将正整数按下列方式分组:(1), (2,3) ,(4,5,6), (7,8,9,10),……;
(1)求第n组的各数之和;(2)问2001属于第几组?
20、(本小题满分12分)
已知:![]()
(1)已知x
1、x 2![]() R且x1+x2=1,求证:f ( x 1 ) + f (x 2 )
=
R且x1+x2=1,求证:f ( x 1 ) + f (x 2 )
=![]() ;
;
(2)求 f (0) + f (![]() ) + f (
) + f (![]() ) +----+f (
) +----+f (![]() ) + f (1).。
) + f (1).。
21、(本小题满分12分),
某房屋开发商出售一套50万元的住宅,可以首付5万元,以后每过一年付5万元,9年后付清;也可以一次付清,并优惠x﹪。问开发商怎样确定优惠率才可以鼓励一次性付款。(按一年定期存款税后利率2﹪,一年一年续存方式计算,x取整数。计算过程中可参考以下数据:1.029=1.19, 1.0210=1.2 , 1.0211=1.24)
22、(本小题满分14分)
.某商品在近30天内每件的销售价格P元与时间t的函数关系是
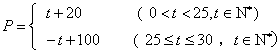
该商品的日销售量Q件与时间t天的函数关系是Q=-t +
40 (0<t≤30, t∈N*![]() ,求这种商品的销售金额的最大值,并指出取得该最大值的一天是30天中的第几天?
,求这种商品的销售金额的最大值,并指出取得该最大值的一天是30天中的第几天?
23.选作题、(本小题满分20分)
设![]()
(1)求f(x)的值域;
(2)证明f(x)为R上的增函数;
(3)若方程f(x2 –2x-a)=0在(0,3)上恒有解,求实数a的取值范围。
参考答案一、C B D A B B B C D D A B
二、13. 28 14.2 15.六项 16. (0,![]() )∪(1,+∞)
)∪(1,+∞)
三、17.解: ![]()
![]()
(I)CRA=![]() ;
(II)CRB=
;
(II)CRB=![]()
∴A∩(CRB)=![]() .
.
18.解:(I)当![]() 时,
时,![]() 即
即![]()
当![]() 时,
时,![]()
解得 ![]() , 于是
, 于是 ![]() ,因此对任何
,因此对任何![]()
(II)![]()
![]() 的前
的前![]() 项和
项和![]()
![]()
![]()
19. (1), (2)63组
20.证明:(1)略
(2)令:![]()
![]()
由(1)得:![]()
∴![]()
![]()
21.解:由题意得
![]() )
)
![]()
![]() =0.8403
=0.8403
∴x% >15.97% 答:一次付款的优惠率应不低于16%
22.解:设日销售金客为M(元),则M与时间t的函数关系为:
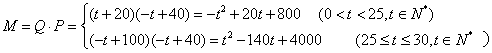
①![]() 时,
时,![]()
当t=10时,M最大=900(元)
②![]()
当t=25时,M最大=1125(元)
综合①、②知:
t=25时,销售金额最大为1125元,取得最大值的是第25天。
23.选作题.解:(1) (-1,1)
(2)略 (3)由于 ![]() ∴
∴![]()
由f(x)的单调性知: x2-2x-a=0 x∈(0,3)
∴a=x2-2x x∈(0,3)
=(x-1)2-1 x∈(0,3)
∴ a∈[-1,3)
∴实数a的取值范围为[-1,3]