任意角的三角函数及同角三角函数的基本关系式
一．知识点
（1）任意角的三角函数的定义：
设
是一个任意角，的终边上任意一点P（除端点外）的坐标是（
，它与原点的距离是
），那么：比值
分别叫的正弦，余弦，正切，余切，正割，余割，记作：sin,
| 三角函数 | 定义域 | 值域 |
|
| R | [-1,1] |
|
| R | [-1,1] |
|
|
| R |
|
| { | R |
|
|
| R |
|
| { | R |
（2）正弦线，余弦线，正切线的定义
（3）三角函数符号的判断
口诀记忆法： 一全正，二正弦，三正切，四余弦
（4）公式一：终边相同的角的同一三角函数值相等
(
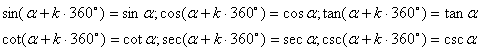(5) 同角三角函数的关系式：
；
; 
, 
, 
; 
二：任意角的三角函数的方法总结
1：用定义法求三角函数值 2．用转化法求终边相同的交的三角函数值
例题：求
的六个三角函数值
例如：求值
3．用分类讨论的方法解题
例如：已知角的终边在直线
上，求角的六种三角函数值
4．用数形结合的方法解三角不等式
例如：已知
，求角
的取值范围
三．同角三角函数的基本关系式的方法总结
1． 用方程的思想指导解题 2. 用整体的思想指导解题
例如：已知
求
例如：已知
求
3． 分类讨论的思想解题 4. 用转化的思想指导解题
例如：已知
，求
。
例如：求证：
四．典型例题
例题1：若角的终边经过点（-2，0），则下列三角函数值不存在的是 （ ）
A B 
C 
D
2．已知角终边上一点P，P与
轴的距离和与
轴距离之比为
且
求和
例题3：设为第二象限角，且
，则
角属于 （ ）
A 第一象限 B 第二象限 C 第三象限 D 第四象限
例题4：已知
，求
例题5：若
，则角的取值范围。
例题6：已知
，则
的值是
例题7：化简：
五：限时训练
1． 已知终边上一点的坐标为（
，则角所在的象限是 （ ）
A 第一象限 B 第二象限 C 第三象限 D 第四象限
2．下列各式中为正值的是 （ ）
A 
B 
C 
D 
3．函数
的值域为 （ ）
A {-2，4} B {-2，0，4} C {-2，0，2，4} D {-4，-2，0，4}
4．角的终边经过点P（
，则
（ ）
A
B
C 
D 
5. 已知是第三象限角，且
，则
（ ）
A
B 
C 
D 
6. 已知
，则
（ ）
A -4 B 4 C -8 D 8
7．求函数
的定义域
8．已知角的终边经过点
，且
，求
的取值范围。
9．若
是方程
的两根，求
的值
10已知
，求
的值